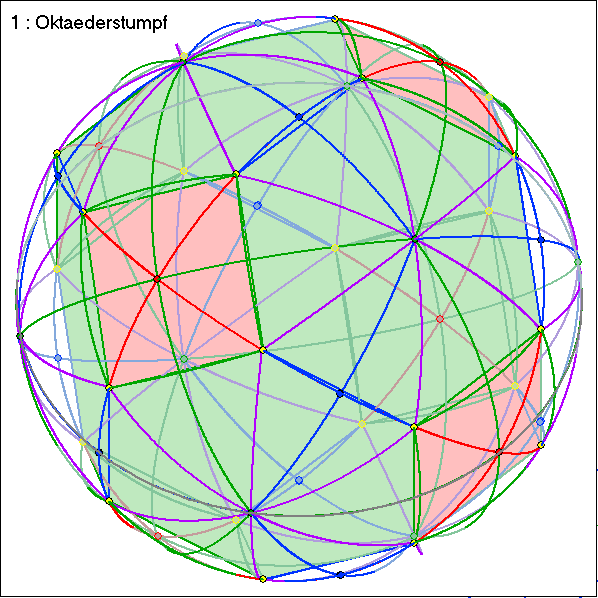
Es lebe die Geometrie!

Archimedische Körper, die aus der Würfel-Kachelung
durch Seiten-Spiegelungen abgeleitet werden können

Die Gleitschau zeigt für die Würfel-Kachelung die Bilder, die auf der vorherigen Seite für die
Tetraeder-Kachelung entsprechend angegeben wurden. Die Erklärungen übertragen sich.

Die Berechnung für den euklidischen Abstand einer Körperfläche F vom Kugel-Zentrum O kann
mit Hilfe des Ausgangs-Dreiecks ABC der Kachelung im Klein-Modell in folgender Weise erfolgen:
Man bestimmt die Koordinaten des gelben A-Eckpunktes P in den sieben ausgezeichneten
Positionen mit Hilfe der Winkelhalbierenden, außerdem die Koordinaten des K-Eckpunkts
Q in Dreieck ABC, für den die Gerade OQ das Zentrum von F trifft. Dann ist der gesuchte Abstand
das Skalarprodukts der Schnittpunkte P' bzw. Q' der Geraden OP und OQ mit der Kugel.
Der Abstand der Körperfläche F vom Kugel-Zentrum O ist also gleich .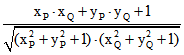
Dies ist der Kosinus-Wert des Bogen-Abstands von P und Q.

Für die Berechnungen im Einzelnen kürzen wir die Wurzel mit w ab
und mit v. Dabei ist der Innenwinkel bei B, der für die Tetraeder-Kachelung den Wert 60°
hat, für die Würfel-Kachelung den Wert 45° und für die Ikosaeder-Kachelung den Wert 36°.

Auf der Seite 'Würfel-Kachelung' wird gezeigt, dass die Eckpunkte A, B und C der Ausgangs-Kachel
im Klein-Modell die Koordinaten , und haben. Die Ebenen durch
O, B, C bzw. O, C, A bzw. O, A, B haben dann die Gleichungen ,
x = 0 und y = 0. Dabei sind die Vorzahlen-Tripel normiert, das heißt, dass die Tripel
, (1 ; 0 ; 0) und (0 ; 1 ; 0) Punkte R, S und T beschreiben, die auf der
Kugel liegen. Auf Grund der Ebenen-Gleichungen sind die Geraden OR bzw. OS bzw. OT
orthogonal zu den Ebenen OBC bzw. OCA bzw. OAB. Darum ergeben sich die Vorzahlen-Tripel
der Winkelhalbierenden durch Addition oder Subtraktion der Vorzahlen-Tripel dieser Ebenen, denn
in einer Raute sind die Diagonalen Winkelhalbierende. Die inneren Winkelhalbierenden durch A, B
und C haben darum die Vorzeichen-Tripel
, und .

Im Klein-Modell errechnet man damit für die gelben A-Eckpunkte in den Positionen '1', '3'. '5' und '6'
die Koordinaten , , und .

Für die Position '1' errechnet man daraus folgende Abstände beim Einsetzen von für P
und den Koordinaten-Tripeln von A, B und C für Q:
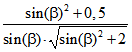, und .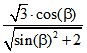
Die erste dieser drei Zahlen gibt den Abstand der blauen Kanten von O an, die zweite den der roten
Flächen und die dritte den der grünen Flächen. Beim Oktaederstumpf sind dies die Zahlen
, und .