Es lebe die Geometrie!

Die Zykloidenverzahnung

Die Zykloidenverzahnung ist nach der Evolventenverzahnung der nächsthäufigste Verzahnungstyp bei
Zahnrädern. Sie wird z. B. bei mechanischen Uhren verwandt. Dabei setzen sich die Zahnflanken aus
Teilen von Zykloidenbögen zusammen. Die folgenden beiden Animationen zeigen Verzahnungen, deren
Kontaktkurve sich aus Kreisbögen zusammensetzt, die sich aber nicht wie bei den alternierenden
2m-Zykloiden zu vollständigen Kreisen schließen.

Die Animation zeigt ein schwarze Zahnstange mit zwei Zahnrädern, bei denen die Zahn-Anzahlen 2 und
3 bzw. drei und vier sind. Die Zahnräder und die Zahnstange haben einen oder drei Berührpunkte-Punkte
mit gemeinsamer Tangente, die entsprechend dem Verzahnungsgesetz orthogonal zur Verbindungsgeraden
der Berührpunkte mit dem Wälzpunkt W im Zentrum der roten Kontaktkurve sind.

Zum Verständnis des s(u)-Graphen oben links stellt man sich einen Punkt P vor, der die Kontaktkurve in
Form einer '8' durchläuft, beginnend bei W, und zwar so, dass der Eckpunkt A oben rechts nach einer
Zeiteinheit erreicht wird, der Eckpunkt B oben links nach zwei und W dann nach drei Einheiten. Analog
werden die Eckpunkte C und D unten rechts und links durchlaufen, so dass für die ganze '8' sechs Einheiten
benötigt werden. Die Größe u auf der Rechtsachse des s(u)-Graphen gibt die laufende Zeit bei diesem
Weg an. s(u) hat die Bedeutung einer Länge. Es ist s(0) = 0 und s(1) die Länge des Bogens WA. Es sei d
der Abstand des rot markierten Mittelpunktes M um Bogen AB von W, r der Radius diese Bogens und b
seine Länge. Dann ist
, , , und .
Eine Begründung hierfür folgt unten auf dieser Seite.

Wenn die Zahnräder sich gleichmäßig um einen Zahn weiterdrehen, bewegt sich in dem s(u)-Graphen die rote
Parallele zur Rechtsachse gleichmäßig um s(6) nch oben. Die Schnittpunkte mit dem Graphen entsprechen
den Kontaktpunkten der Zahnräder. Wenn der u-Wert eines Schnittpunktes zwischen 0 und 1 liegt, teilt er
das Intervall [0 ; 1] im gleichen Verhältnis wie der zugehörige Kontaktpunkt den Bogen WA teilt. Wenn der
u-Wert zwischen 1 und 2 liegt gilt Entsprechendes für den Bogen AB, usw..

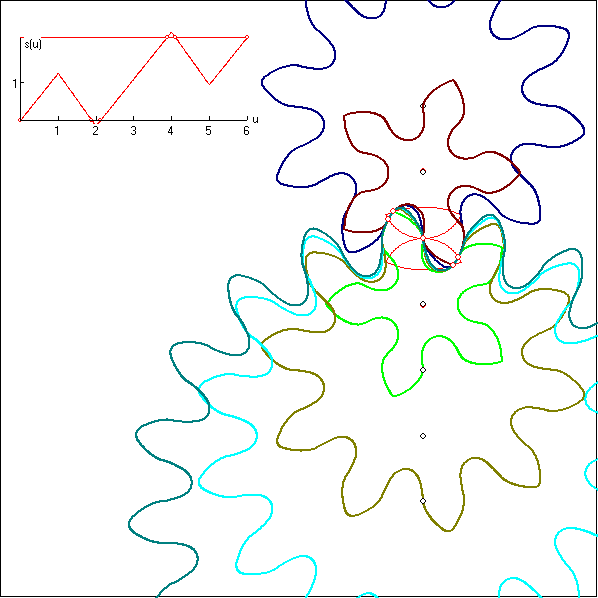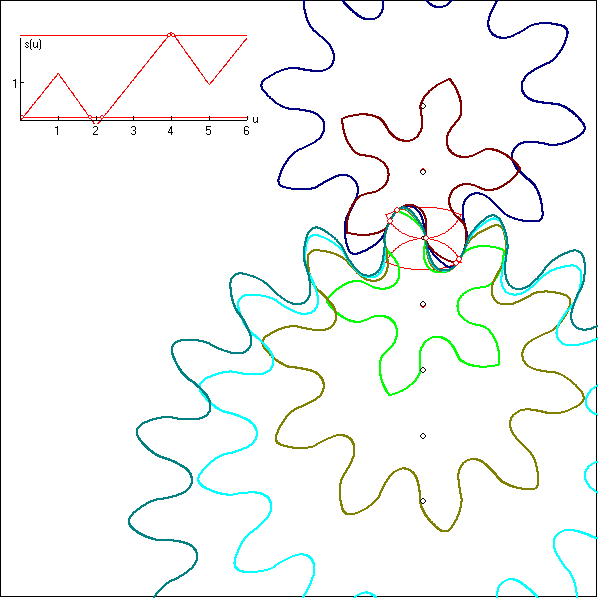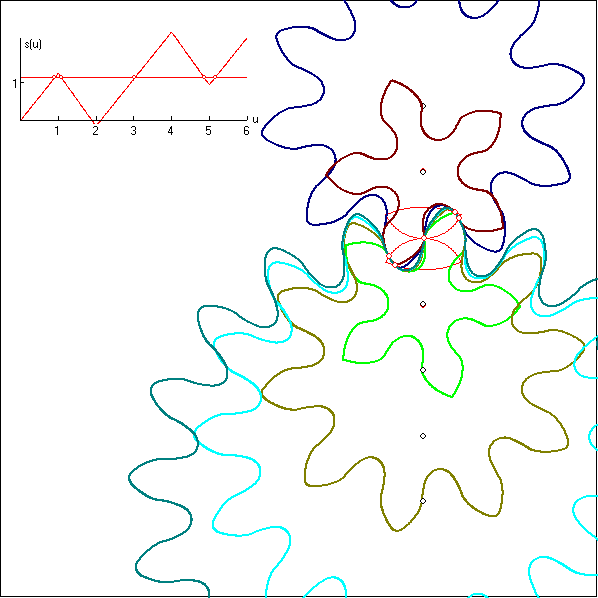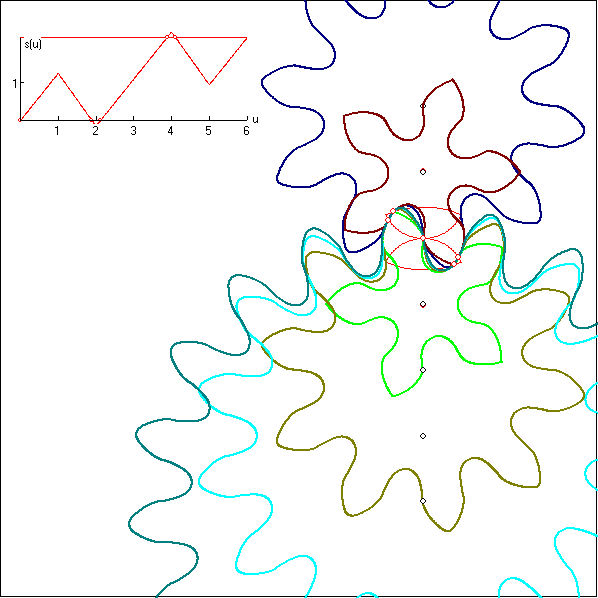
Hier wurde bei der Kontaktkurve der Bogens AB flacher gemacht mit dem Effekt, dass im s(u)-Graph
die Abschnitte im u-Intervall [1 ; 2] und [4 ; 5] im Betrag steiler wurden. Dadurch erhöht sich die Anzahl
der möglichen Kontaktpunkte.

Im Folgenden soll die Bedeutung des s(u)-Graphen geklärt werden.

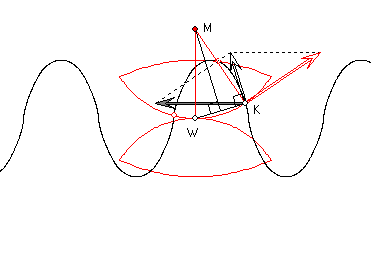
Diese Slideshow zeigt Zeichnungen zur Erklärung eines Verfahrens, mit dem man ausgehend von der
roten Kontaktkurve dazu gehörige Verzahnungskurven so zeichnen kann, dass das Verzahnungsgesetz
erfüllt ist. Dieses besagt, dass die Tangente im Kontaktpunkt K zweier Zahnräder stets orthogonal zur
Verbindungsgeraden von K mit dem Wälzpunkt W stehen soll. Die ersten sechs Bilder der Slideshow
beziehen sich nur auf die Zeichnung der schwarzen Zahnstange, das siebente Bild bezieht das blaue
Zahnrad mit ein. Die Kontaktkurve setzt sich aus Kreisbögen zusammen und hat W als Symmetriepunkt.

Zu den ersten sechs Bildern stellt man sich vor, dass sich ein Stift im Punkt K auf einer Schiene in Form
der Kontaktkurve bewegt, beginnend bei W und dann wie bei einer '8' über die Eckpunkte A, B, zurück
zu W und weiter über die Eckpunkte C und D. Der Stift soll dabei auf einer Zeichenunterlage die Kurve
der Zahnstange zeichnen. Damit das möglich ist, muss sich die Zeichenunterlage während der Bewegung
des Stiftes parallel zur Rechtsachse vor oder zurück bewegen. Diese Bewegung soll so erfolgen, dass der
momentane Strich, den der Stift zeichnet stets orthogonal zur Geraden KW ist. Dazu müssen der rote
Geschwindigkeitsvektor des Stifte relativ zur Schiene und der schwarz-graue Geschwindigkeitsvektor
des Stiftes relativ zur Zeichenfläche so zusammenwirken, dass der Vektor senkrecht zu KW steht.
Die ersten drei Bilder zeigen die Lösung für K zwischen W und A. Die Zeichenfläche muss sich dann nach
rechts bewegen, so dass nach links zeigt. Beide Vektoren haben die gleiche Länge, da das Dreieck aus
den Punkten W, K und dem zum Bogen KW gehörigen Mittelpunkt M gleichschenklig ist. Beim Weg des
Stiftes von W nach A wird darum die Zeichenfläche um die Länge des Bogens WA verschoben. Das
vierte bis sechste Bild zeigen die Lösung für K zwischen A und B. Dann muss das von den Vektoren und
aufgespannte Dreieck ähnlich zum Dreieck MKW sein. Wenn d der Abstand von M und W ist und
r der von M und K, dann folgt, dass sich die Längen von und wie d zu r verhalten. ist dabei nach
rechts gerichtet, da sich die Zeichenfläche nach links bewegen muss, und zwar um die Länge . Bei
einem vollen Umlauf des Stifts in Form einer '8' verschiebt sich die Zeichenfläche insgesamt um die Länge
. Dies ist die Länge eines Zahnabschnitts, die in der Getriebelehre als 'Teilung' bezeichnet
wird. Im s(u)-Graph erscheint sie als Differenz s(6)-s(0).

Das siebente Bild zeigt den Zusammenhang mit dem blauen Zahnrad. Zum Zeichnen der blauen Kurve mit
dem Stift, der sich auf der Kontaktkurven-Schiene bewegt, muss sich die Zeichenfläche um dessen Drehpunkt
R drehen. Der blaugefüllte Vektor der Relativgeschwindigkeit des Stifte gegenüber der Zeichenfläche
muss so lang sein, dass der Vektor ebenfalls senkrecht zu KW steht, damit das Verzahnungsgesetz
erfüllt ist. Das wird erreicht, wenn das von und aufgespannte Dreieck ähnlich zum Dreieck RWK ist.
Die Längen von und verhalten sich dann wie die Streckenlängen KR und WR. Der Abstand WR ist
der Radius des Wälzkreises des Zahnrades. Die Zeichenfläche muss sich mit einer Winkelgeschwindigkeit
drehen, die sich ergibt, wenn man den Betrag von durch teilt. Im Wälzpunkt W stimmt darum die
Geschwindigkeit der Zeichenfläche bei der Rotation um R mit der bei der Verschiebung parallel zur Rechts-
Achse überein. Bei einem vollen Umlauf des Stiftes bewegt sich darum ein Punkt auf dem Wälzkreis um die
Bogenlänge weiter.

Die folgende Animation zeigt eine Möglichkeit, wie die Kurven bei einer stehenden Zeichenfläche gezeichnet
werden können.