Es lebe die Geometrie!

Der Satz von Holditch

Der Satz des englischen Mathematikers Hamnet Holditch (1800 - 1867) wird hier in einer Abwandlung
einer Formulierung von Arne Broman (Holditch’s Theorem. A fresh look at a long forgotten theorem,
Mathematics Magazine, Vol. 54, 1981) angegeben. Unter dem signierten Inhalt der von einem geschlossenen
stetigen Wegs umschlossenen Fläche verstehen wir dabei das Stieltjes-
Integral . Im Fall eines konvexen geschlossenen Wegs, der gegen den Uhrzeigersinn durchlaufen
wird, ist dies ein Flächeninhalt im gewöhnlichen Sinn. Dieser verdoppelt sich, wenn die Fläche vom Weg
zweimal umrundet wird, und muss mit -1 multipliziert werden, falls man den Umlaufsinn umkehrt. Wenn der
Weg z. B. die Form einer 8 hat, setzt sich der signierte Inhalt aus der Differenz der Inhalte (im gewöhnlichen
Sinne) von den beiden umrundeten Teilflächen zusammen.


Satz : Es sei ein geschlossener stetiger Weg endlicher Länge in der
Ebene, der eine Fläche mit dem signierten Inhalt einschließt. sei eine stetige Funktion
mit beschränkter Variation und . Mit zwei Konstanten s und u sei definiert:
und .
Für alle hat also die Strecke A(t)B(t) die konstante Länge s und wird vom Punkt C(t) so innen oder
außen geteilt, dass der Abstand dieses Punktes von A(t) bzw. B(t) durch die Konstanten bzw.
gegeben ist. bzw. sei der signierte Flächeninhalt der vom Weg bzw.
eingeschlossenen Fläche.
Aus folgt dann .


In der klassischen Formulierung von Holditch stimmen die Punktmengen der Wege und
überein und sind konvex. Ein Beweis des hier formulierten Satzes wird am Schluss dieser Seite angegeben.
In den folgenden Animationen sind die Punkte A und B dunkelrot bzw. hellrot eingezeichnet und der Punkt C
grün. Die hellblau markierte Fläche hat stets den Flächeninhalt . Sie stimmt mit dem
Inhalt der Ellipse überein, die als grau-karierte Fläche dargestellt ist. Diese Ellipse hat die Längste der Strecken
AB, AC und BC als Durchmesser. Für u > 1 hat der zugehörige konjugierte Durchmesser die Länge
, für u zwischen 0 und 1 die Länge und für u < 0 die Länge
.

Die Punkte A und B bewegen sich hier auf dem roten Quadrat. Die Seitenlänge stimmt mit der Länge s
der Strecke AB überein. Bei den vier Umläufen der Strecke hat der Parameter u nacheinander die Werte
0,5 ; 0,25 ; 4/3 und 2. Für u = 0,5 und u = 4/3 ergibt sich für die karierte Ellipse ein Kreis, dessen Radius
im ersten Fall gleich dem der grünen Kreisbögen der Spur von C ist. Diese Spur setzt sich in jedem Fall aus
Ellipsenbögen zusammen. Die blau gezeichnete Hüllkurve (Enveloppe) der Geradenschar A(t)B(t) besteht
aus Astroiden-Bögen.

Das Quadrat wurde hier durch ein gleichseitiges Dreieck ersetzt, dessen Umkreis-Radius mit der
Länge s = 1 der Strecke AB übereinstimmt. Bei den drei Umläufen der Strecke hat der Parameter u
die Werte 0,5 ; 0,75 und 4/3. Für u = 0,5 und u = 4/3 ist die karierte Ellipse, deren Flächeninhalt
mit dem der hellblauen Fläche übereinstimmt, ein Kreis. Die grüne Spurkurve von C setzt sich aus
Strecken und Ellipsenbögen zusammen. Die Halbachsen der zugehörigen Ellipsen haben für u = 0,5
die Hälfte und 1/6 von der Länge der Dreieck-Seiten. Für u = 0,75 sind die Halbachsen-Längen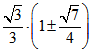
, und für u = 4/3 sind sie .

Die rote Ellipse hat die Halbachsen-Längen 1 und 0,5. Die Länge der Strecke AB beträgt s = 0,9.
Bei den beiden Umläufen der Sehne sind die Werte des Parameters u gleich 0,5 und 0,146. Die
karierte Ellipse ist im ersten Fall ein Kreis und im zweiten eine zur roten Kurve ähnliche Ellipse.

Hier wird die Sehne AB der roten Ellipse durch C außen geteilt mit dem Parameter u = -1/3 bzw. u = 2.

Die rote Kardioide entsteht dadurch, dass ein Rollkreis vom Radius 1 außen an einem Gangkreis vom
Radius 1 ohne zu Rutschen abrollt und dabei ein Randpunkt eine Spur zeichnet. Die Sehne AB hat
die Länge 4. Falls die Sehne durch die Spitze der Kardioide geht, ist sie eine 1-Hauptsehne. Bei den
beiden Umläufen hat der Parameter die Werte u = 0,5 und u = 0,25. Im ersten Fall ist der Gangkreis
ein Teil der grünen Spurkurve des Punktes C. Da der Inhalt der von der Kardioide berandeten Fläche 6
mal so groß ist wie die des Gangkreises und die hellblaue Fläche nach dem Satz von Holditch den 4-fachen
Inhalt des Gangkreises hat, ist die Fläche der halbmondförmige Teil der grünen Kurve so groß wie die des
Gangkreises.

Die Länge der Kardioiden-Sehne AB ist hier s = 3. Bei den beiden Umläufen hat der Parameter u
die Werte -1/3 und 0,5. In beiden Fällen ist die karierte Ellipse ein Kreis. Im ersten Fall stimmt der
Flächeninhalt des Kreises mit dem der hellblauen Fläche überein. Im zweiten Fall ist der Inhalt des
Kreises so groß wie die Differenz von den Inhalten der rot bzw. grün gestreiften Fläche.


Zum Beweis des Satzes von Holditch :

Das Stieltjes-Integral ist linear im Integranden x(t) und auch linear im Integrator y(t), d. h. es gelten die
Gleichungen
und .
Wegen folgt für den signierten Inhalt
der vom Weg eingeschlossene Fläche


, wobei sich die Bedeutung dieser Größen aus der Gleichung ergibt.

Für u = 1 ist Darum gilt und . Der Satz von Holditch
folgt nun aus .