Es lebe die Geometrie!

Hypozykloide mit fünf Spitzen
(hier auch -5-Zykloide genannt)
Die rot gezeichnete Hypozykloide mit fünf Spitzen entsteht durch Abrollen von Gangkreisen mit den
Radien 1/5 oder 4/5 an dem dick schwarz gezeichnete Rastkreis hat den Radius 1. Die zugehörigen roten
Pfeile haben Winkelgeschwindigkeiten im Verhältnis 1 zu -4. Wenn bzw. der Richtungswinkel des
langen bzw. kurzen roten Pfeils ist, dann ist . Der Richtungswinkel des Geschwindigkeitsvektors
vom Spurpunkt der Zykloide erfüllt dann die Gleichung , da dieser Vektor sich als
Resultierende zweier gleich langer Vektoren ergibt, die senkrecht zu den roten Pfeilen gerichtet sind.

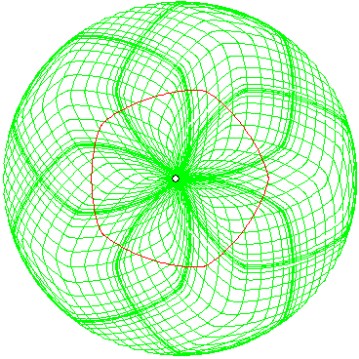
Neben der rot gezeichneten -5-Zykloide zu den Gangkreisradien 1/5 und 4/5 tritt hier eine zweite
Zykloide mit fünf Spitzen auf, die ebenfalls durch Abrollen eines Gangkreises im Innern des Rastkreises
entsteht und hier grün gezeichnet ist. Die Gangkreisradien sind hierbei 2/5 oder 3/5. Wir
nennen sie {-5;+5}-Zykloide, weil sie einen analogen Zusammenhang mit der Epizykloide mit fünf
Spitzen hat, die durch Abrollen eines Gangkreises an der Außenseite des Rastkreises entsteht und hier
+5-Zykloide genannt wird. Die entsprechende {-3;+3}-Zykloide stimmt mit der Steiner-Zykloide überein.

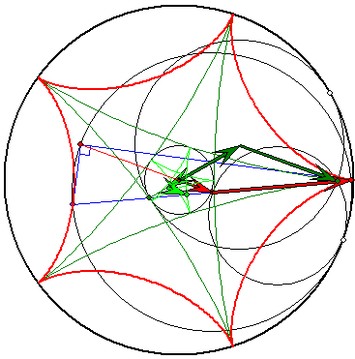
-5-Zykloide und {-5;+5}-Zykloide
Die -5-Zykloide entsteht durch Abrollen eines
Gangkreises mit dem Radius 1/5 oder 4/5. Der
zum kleineren Gangkreis gehörige doppelt so
große Gangkreis mit dem gleichen Rastkreis-
Berührpunkt hat den blau gezeichneten Durchmesser,
der die grüne {-5;+5}-Zykloide berührt.

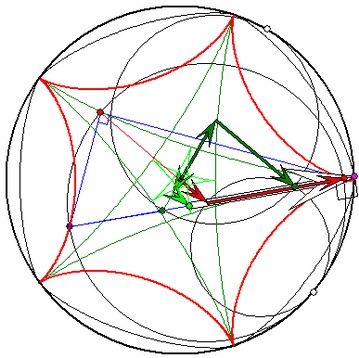
Evolvente der {-5;+5}-Zykloide
Der dunkelgüne Pfeilzug mit Pfeilen der Längen
2/5 und 3/5 erzeugt die {-5;+5}-Zykloide, der
hellgrüne mit den Längen 2/25 und 3/25 die
Evolvente dazu. Der an den markierten Punkt
der Evolvente angesetzte weißgefüllte Pfeil mit
der Länge 24/25 hat seine Spitze auf dem
Gleichdick, das zu der {-5;+5]-Zykloide gehört
und die Evolvente durch eine Spitze dieser
Zykloide ist.

In dieser Animation wird neben der -5-Zykloide auch die +5-Zykloide gezeichnet, die dadurch entsteht,
dass neben einem Gangkreis mit dem Radius 1/5 im Innern des Rastkreises ein weiterer mit gleicher
Größe außen abrollt. Anders als bei der Steiner-Zykloide ist die Verbindungsgerade der die Spur
zeichnenden roten Punkte P und Q keine Tangente der -5-Zykloide, wohl aber Tangente der
{-5;+5}-Zykloide. Wie bei der Steiner-Zykloide ist diese Gerade aber orthogonal zu der Verbindungs-
geraden der Rastkreis-Berührpunkte der größeren Gangkreise mit den Radien 4/5 und 6/5. Der Punkt R,
der die Strecke PQ im Verhältnis 3 : 2 = (5+1) : (5-1) teilt, liegt auf dem zugehörigen Gleichdick. Die
Gerade PQ berührt die {-5;+5}-Zykloide im Punkt S, der die Strecke PQ außen im Verhältnis -3 : 2 teilt.
S ist also der vierte harmonische Punkt zu P, Q; R.

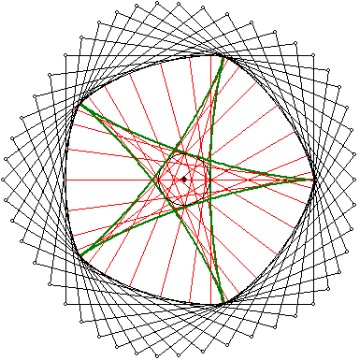
Gleichdick mit Quadraten
Die Breite des zur{-5;+5}-Zykloide gehörigen
Gleichdicks beträgt 48/25. Die Mittelpunkte der
umschließenden Quadrate liegen auf einem Kreis
um den Urspung mit dem Radius 1/25.

Minkowski-Addition vom Gleichdick
mit seinem Spiegelbild
Die Minkowki-Addition ergibt wie bei
jedem Gleichdick einen Kreis. Zur Darstellung
wurde die Mitte eines grünen Punktspiegelbilds des
roten Gleichdicks auf dessen Rand verschoben.