Es lebe die Geometrie!

Analogon der Satzes von Ceva für ein Viereck ABCD,
mit Eckpunkten, die nicht in einer gemeinsamen Ebene liegen

Wenn man eine Gerade in irgendeiner Weise im Raum bewegt, nennt man die Menge der dabei getroffenen
Punkte eine Regelfläche. Auf dieser Seite betrachten wir dazu die Verbindungs-Gerade eines beweglichen
Punktes P auf der Geraden AB mit dem beweglichen Punkt Q auf der Gerade CD, wobei A, B, C und D
fest bleiben. Dabei bewegen sich P und Q nicht unabhängig voneinander, sondern so, dass das Produkt der
Teilverhältnisse von P auf AB und Q auf CD konstant bleibt. Die Konstante bezeichnen wir mit tvk. Für P
auf der Geraden AB ist das Teilverhältnis von P auf der gerichteten Strecke AB der Quotient der Abstände
P von B und P von A. Dieser Quotient ist also nicht negativ. Für P außerhalb der Strecke AB wird dieser
Quotient mit einemMinus-Zeichen versehen. Wenn B zwischen A und P liegt, ist das Teilverhältnis also
eine Zahl zwischen-1 und 0, wenn A zwischen P und B liegt, eine Zahl kleiner als -1. Für P = A ist das
Teilverhältnis unendlich.Wenn p bzw. a bzw. b das Koordinaten-Tripel von P, A und B ist und
gilt, dann ist das Teilverhältnisse von P auf AB gleich .
Bei der Angabe des Teilverhältnisses ist AB von BA zu unterscheiden, denn das Teilverhältnis von P auf
der gerichteten Strecke BA ist der Kehrwert des Teilverhältnisses von P auf der gerichteten Strecke AB.

Wenn das Produkt der Teilverhältnisse von P auf AB und Q auf CD konstant tvk ist, führt dies dazu, dass
man die gleiche Regelfläche analog mit Hilfe zweier Punkte R und S auf den Geraden DA bzw. BC erzeugen
kann, für die das Produkt der Teilverhältnisse von R auf DA und S auf BC konstant der Kehrwert von tvk
ist. Dies ist eine Folgerung aus dem Analogon der Satzen von Ceva (1647-1734) für das Viereck ABCD.
(Siehe zum klassischen Satz von Ceva Satz1 in ' Schwerpunktskoordinaten in der Dreiecksgeometrie'
--> https://www.vivat-geo.de/Pdf-Dateien/Schwerpunktskoordinaten.pdf )

Satz : ABCD sei ein rämliches Viereck mit nicht komplanaren Eckpunkten zu den
Koordinaten-Tripeln a, b, c und d. Sei P auf AB, Q auf CD , R auf DA und S auf BC.
Sei P ungleich A, Q ungleich C , R ungleich D und S ungleich B.

1. Dann schneiden sich die Geraden PQ und RS oder sie sind parallel genau dann,
wenn das Produkt der Teilverhältnisse von P auf AB, S auf BC, Q auf CD,
bzw. R auf DA gleich 1 ist.

2. Wenn ist, dann ist
kartesisches Tripel des Schnittpunkts T der Geraden PQ und RS , falls ist;
andernfalls sind PQ und RS parallel mit dem Richtungs-Vektor .


Hier wird also das Koordinaten-Tripel t vom Schnittpunkt T als Linearkombination von den vier Tripeln
a, b, c und d dargestellt, mit der Neben-Bedingung, dass die Summe der Vorzahlen gleich 1 ist. Wenn man
jedes Tripel um eine vierte Komponente zu einem Quadrupel , , , und erweitert, ergibt sich
die Gleichung für die man keine
Neben-Bedingung mehr formulieren muss, weil sie schon in der Gleichung durch die vierten Komponenten
erfasst wird. Man benutzt diese Quadrupel zur Beschreibung der Punkte A, B, C und D und T im
dreidimensionalen projektiven Raum. Dabei wird zugelassen, dass man die Komponenten eines Quadrupels
mit der gleichen Zahl r multipliziert. Denn man kann durch r wieder teilen, um das Quadrupel mit der vierten
Komponente 1 zu rekonstruieren. Ein Quadrupel (x;y;z;0) mit der vierten Komponente Null beschreibt im
projektiven Raum den 'unendlich fernen' Punkt, der auf allen Geraden mit dem Richtungs-Vektor (x;y;z) liegt.

M sei die Matrix, deren Zeile die Quadrupel , , und sind. Für das Quadrupel
gilt dann , also , wobei
wir den tiefgestellten Punkt zur Bezeichnung der Matrix-Multiplikation benutzen und q als Matrix mit
einer Zeile ansehen. Sowohl q als auch sind Quadrupel zur Bescheibung des Punktes T. Zur
Unterscheidung nennen wir 'kartesisches' Quadrupel und q 'baryzenrisches' Quadrupel oder Quadrupel
in 'Schwerpunkts-Koordinaten' zur Basis Statt q benutzen wir die Bezeichnung mit
hochgestelltem b für 'baryzentrisch'.

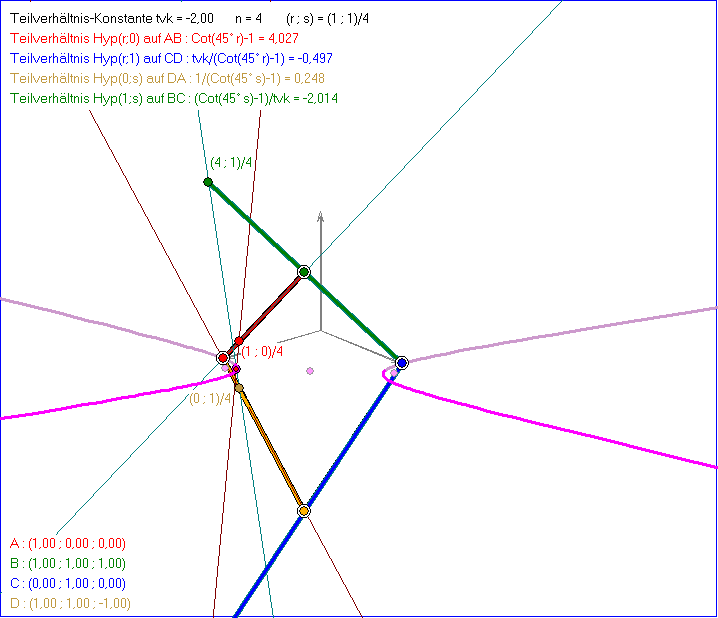
Die Gleitschau zeigt das Viereck ABCD mit Eckpunkten A, C in den Einheitspunkten der x- bzw.
y-Achse, den Punkt B = (1;1;1) und den Punkt D, der durch Spiegelung von B an der xy-Ebene
entsteht. Wir nennen dieses Viereck im Folgenden 'Standard-Viereck'. Auf der Geraden AB wird
der Punkt P = Hyp(r ; 0) bewegt, wobei r die Zahlen der Menge durchläuft
und das Teilverhältnis auf AB angibt, so dass für das Koordinaten-Tripel p gilt:
. Dabei bewegt sich der Punkt Q = Hyp(r ;1) auf der Geraden CD , so dass das
Teilverhältnis auf CD der Quotient der Teilverhältnis-Konstanten tvk und des Teilverhältnisses vr von P
auf AB ist. Dann ist das Koordinaten-Tripel von Q gleich . In der ersten Phase
der Gleitschau ist tvk = 2. Gleichzeitig mit der Bewegung von P und Q verschiebt sich der Punkt
R = Hyp(0 ; s) (mit s = r) so auf DA, dass das Teilverhältnis auf DA der Kehrwert des
Teilverhältnisses vr von P auf AB ist. Zur Festlegung des Teilverhältnisses des
Punktes S = Hyp(1 ; s) auf BC (mit s = r) wird vr durch tvk geteilt.

Der magentafarbene Punkt T = Hyp(r ; r) ist der Schnittpunkt der braunen Gerade PQ und der grünblauen
Geraden RS . Dieser Punkt bewegt sich bei tvk = 2 auf dem Einheitskreis um den Ursprung in der xy-Ebene.
Der Mittelpunktwinkel zwischen A und T hat die Größe , der magentafarben angezeigte Winkel ist halb
so groß, also . Im zweiten Teil der Gleitschau wird der Vorgang aus der Vogel-Perspektive gezeigt. Man
erkennt daran, warum die Wahl des Teilverhältnisses mit wachsendem r ein proportionales
Wachsen des Mittelpunktswinkels bewirkt.

Im zweiten Teil der Gleitschau wird die Teilverhältnis-Konstante schrittweise bis tvk = 1 vermindert.
Die magentafarbene Kurve ist für tvk>1 eine Ellipse und für tvk = 1 eine Parabel mit der Geraden y = x
als Symmetrieachse. Die Parabel hat die Gerade y =2-x als Leitgerade, ihr Scheitelpunkt ist ,
ihr Brennpunkt und ihre Gleichung .

Der gleiche Ablauf wie in der vorhergehenden Gleitschau wird hier mit Teilverhältnis-Konstanten
-tvk statt tvk gezeigt. Die magentafarbene Kurve ist hier eine Hyperbel.

In dieser Animation wird das Standbild zu r = 15/4 für Teilverhältnis-Konstanten tvk zwischen 2,5 und 0,2
variiert. Die magentafarbene Kurve ist für tvk > 1 eine Ellipse, für tvk = 1 eine Parabel und für tvk < 1 eine
Hyperbel in der xy-Ebene mit der Geraden y = x als Symmetrie-Achse. Die Gleichung dieses Kegelschnitts ist
. Der Mittelpunkt ist für tvk ungleich 1 der Punkt .
Er teilt die Strecke zwischen den Mittelpunkten von AC und BD im Verhältnis -tvk. Dies gilt nicht nur für das
Standard-Viereck, sondern für jedes räumliche Viereck mit nicht komplanaren Eckpunkten. Die Achsenabschnitte
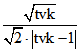sind und 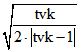, wobei für tvk<1 der zweite Wert der Nebenachsen-Abschnitt
der Hyperbel ist. Im Fall tvk = 1 beträgt der Abstand des Brennpunkts von dem Scheitelpunkt .

In dieser Animation wird das 15. Bild der ersten Gleitschau für die Teilverhältnis-Konstante tvk von
2,0 bis 0,2 verändert und dann in die Vogel-Perspektive gewechselt. Anschließend wird der Rückweg
mit verdoppelter Anzahl der Geraden gezeigt. Gegenüber der vorangehenden Animation sind alle
Schnittpunkte der Geraden angegeben. Dabei zeigt sich, dass jede braune Gerade jede grünblaue
Gerade schneidet und umgekehrt. Dagegen schneiden sich verschiedene Geraden gleicher Farbe nie.
Jede braune Gerade verbindet einen Punkt P = Hyp(r ; 0) auf AB mit einem Punkt Q = Hyp(r ;1) auf
CD und jede grünblaue Gerade einen Punkt R = Hyp(0 ; s) auf DA mit einem Punkt S = Hyp(1 ; s) auf
BC. Dass sich diese Geraden genau dann schneiden, wenn sie unterschiedliche Farbe haben, gilt auch dann,
wenn man nicht nur die r- und s-Werte der Animation wählt, sondern dies gilt für alle reelle r und s. Dabei
kommt es allerdings vor, dass verschiedenfarbige Geraden parallel sind. In dem Fall betrachtet man den
zugehörigen unendlich fernen Punkt als Schnittpunkt.

Der Punkt P = Hyp(r ; 0) auf AB hat das Koordinaten-Tripel .
Q = Hyp(r ;1) auf CD hat das Koordinaten-Tripel .
R = Hyp(0 ; s) auf DA hat das Koordinaten-Tripel
und S = Hyp(1 ; s) auf BC hat das Koordinaten-Tripel .

Die braune Gerade durch P und Q nennen wir Gx(r), die grünblaue durch R und S Gy(s).
Sei wieder und analog .
Der Schnittpunkt Hyp(r;s) von PQ und RS hat dann das Koordinaten-Tripel


Für ein beliebiges nicht komplanares Viereck ABCD kann diese Konstruktion analog durchgeführt
werden, auch mit beliebigen Werten von vr und vs, die nicht mit der Kotangens-Funktion definiert
sind. Wenn (ax;ay;az) Koordinaten-Tripel von A ist und Analoges für B, C und D gilt, dann hat der
Schnittpunkt von PQ und RS das (kartesische) Koordinaten-Tripel

und das baryzentrische Quadupel zur Basis .

Die Geraden Gx(r) entsprechen in der Ebene mit den Koordinaten x und y den Geraden mit der
Gleichung x = r, und die Geraden Gy(s) denen mit der Gleichung y = s. Wir nennen r und s
'Hyperboloid-Koordinaten'. Die Menge der Geraden Gx(r) für relle Zahlen r bezeichnet man als
'Regulus', auch die Menge der Geraden Gy(s).

Die Vereinigung der Punktmengen jedes dieser beiden Regulusse (Reguli) ist eine Quadrik QH mit der
Gleichung für das Standard-Viereck. Wenn das
Quadrupel (ax;ay;az;1) bezeichnet, das Quadrupel (x ; y ; z ; 1) und analog mit b, c und d verfahren
wird, gilt für die Gleichung von QH bei einem beliebigen nicht planaren Vierecks ABCD
.
Wenn man die Punkte nicht wie in dieser Gleichung mit kartesischen Quadrupeln beschreibt, sondern mit
den oben beschriebenen baryzentrischen Quadrupeln, und (xb;yb;zb;ub) das baryzentische Quadrupel
zu dem Punkt mit dem kartesischen Quadrupel ist, dann vereinfacht sich die Gleichung zu
.

Für tvk ungleich 1 ist QH ein einschaliges Hyperboloid und sonst ein hyperbolisches Paraboloid. Wenn
Der Punkt A im Koordinaten-Ursprung liegt und die Punkte B, C und D bei den Einheit-Punkten der
x- bzw. y- bzw. z-Achse, dann ergibt sich für QH die Gleichung .

Wir betrachten im Folgenden wieder das Standard-Viereck ABCD.

Die xy-Ebene und die Ebene mit der Gleichung x = y sind dann für alle Werte von tvk Symmetrieebenen.
Die magemtafarbene Kurve Km und die hellgrüne Kurve Kg des Schnitts der Quadrik mit der xy-Ebene
bzw. der Ebene x = y legen die Quadrik eindeutig fest. Diese beiden Ebenen sind euklidisch orthogonal.
Km ist für 1< tvk eine Ellipse, für tvk = 1 eine Parabel und für tvk < 1 eine Hyperbel, Kg für 1 < tvk eine
Hyperbel, für tvk = 1 eine Parabel, für 0 < tvk < 1 eine Ellipse und für tvk < 0 eine Hyperbel. Beide
Kurven haben für tvk<>1 den gleichen Mittelpunkt . Die violette Kurve Kv
(bei tvk<>1) ergibt sich als Schnitt der Quadrik mit der Ebene durch Z, die euklidisch orthogonal zu
den Ebenen von Km und Kg ist. Sie ist für tvk > 0 eine Hyperbel und für tvk < 0 eine Ellipse.

Die letzten 19 Bilder der Gleitschau zeigen die drei Kurven auch für den Fall tvk < 0.

Wir setzen im Folgenden tvk <> 1 voraus.
Sei , , und .
Durch eine Koordinaten-Transformation, welche die euklidische Abstandsberechnung unverändert lässt,
kann der Term der Quadrik QH in den Term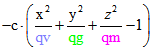
trasformiert werden. Wenn man in diesem zweiten Term x und y durch
bzw. ersetzt, erhält man den ersten Term.


Für 1 < tvk ist 0 < qv , 0 < qg und qm < 0. Km ist dann eine Ellipse mit einem gemeinsamen Scheitelpunkt
mit Kg und Kv im Abstand bzw. von Z. ist für Kg und Kv der
zweite Achsenabschnitt.

Für 0 < tvk < 1 ist 0 < qv , qg < 0 und 0 < qm . Kg ist dann eine Ellipse mit einem gemeinsamen Scheitelpunkt
mit Kv und Km im Abstand sv bzw. sm von Z. sg ist für Kv und Km der zweite Achsenabschnitt.


Für tvk < 0 ist qv < 0, 0 < qg und 0 < qm . Kv ist dann eine Ellipse mit einem gemeinsamen Scheitelpunkt
mit Km und Kg im Abstand sm bzw. sg von Z. sv ist für Km und Kg der zweite Achsenabschnitt.

Zur Quadrik QH des Standard-Vierecks passend definieren wir symmetrische Bilinearformen f, fp, fg und gg,
welche die Orthogonalität von Ebenen, die Polarität von Punkten, sowie die Orthogonalität und das Schneiden
von Geraden im dreidimensionalen projektiv-metrischen Raum beschreiben. Dabei werden also Punkte durch
Quadrupel beschrieben, deren vierte Komponente genau dann Null ist, wenn es sich um einen unendlich fernen
Punkt handelt. Für endliche Punkte kann man das Quadrupel durch die vierte Komponente teilen und erhält
dann in den ersten drei Komponenten ein Tripel des affinen Raums. Ein (kartesisches) Ebenen-Quadupel
gehört zu der Ebenen mit der Gleichung , falls , und
nicht alle drei Null sind, andernfalls beschreibt das Quadrupel die 'unendlich ferne' Ebene, vorausgesetzt, dass
nicht auch gleich Null ist.

Sei 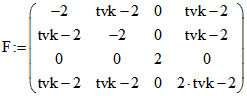und für Ebenen-Quadrupel d und e. Den
tiefgestellten Punkt benutzen wir auch hier als Verknüpfungs-Zeichen für die Matrizen-Multiplikation und
sehen die Zeile d und die transponierte Spalte als Matrizen an. Die zu d und e gehörigen Ebenen D und E
sind genau dann orthogonal in der zu QH passenden Maß-Bestimmung, wenn f(d;e) = 0 ist. Wir verwenden
dafür die Bezeichnung ' Hyperboloid-orthogonal ', kurz ' H-orthogonal '. Das (kartesiche) Punkt-Quadupel d.F
gibt den 'H-Pol' von D an. Eine Ebene E ist genau dann H-orthogonal zu D, wenn E mit diesem H-Pol inzidiert.
Die Ebenen der Kegelschnitte Km , Kg und Kv sind sowohl H-orthogonal als auch euklidisch orthogonal.

Sei für Punkt-Quadrupel p und q. Die zugehörigen Punkte P und Q heißen
zueinander 'H-polar', wenn f(p;q) = 0 gilt. Die Punkte der Quadrik QH sind genau die zu sich selbst
H-polaren Punkte.

Eine Gerade beschreiben wir durch ein Tripel-Paar aus Plücker-Koordinaten. Siehe dazu
'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum I'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf.
Die dort angegebene Definition der Polarität von Geraden verallgemeinern wir in folgender
Weise für eine Matrix F, die nicht notwendig nur Nullen außerhalb der Hauptdiagonalen hat :
C*(F) sei die Matrix der Minoren 2. Stufe von F zu der Index-Folge 12, 13, 14, 23, 24, 34,
wie sie zum Beispiel im Algebra-Programm Mathematica benutzt wird. Die Komponenten von
C*(F) sind also die Determinanten der Unter-Matrizen von F, die entstehen, wenn man die
Kreuzungsstellen eines Zeilen-Paars zum Index-Paar i j und eines Spalten-Paars zum Index-Paar
k l herausgreift und diese Zahlen in der angegebenen Index-Folge in einer Matrix mit sechs Zeilen
und Spalten anordnet. Wir variieren diese Index-Folge zu der Folge 23, 31, 12, 41, 42, 43,
indem wir C*(F) mit der Permutations-Matrix
transformieren zu .
Zum Tripel-Paar einer Geraden h definieren
wir das Tripel-Paar der zu h ' H-polaren ' Geraden durch
,
wobei gilt.
Für die oben angegebene Matrix F ergibt sich dann das Tripel-Paar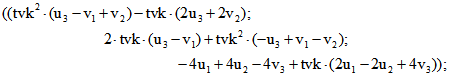
.
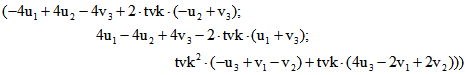ist ebenfalls ein Tripel-Paar von h.
Wenn eine Ebene D, welche die Gerade h ganz enthält, um h gedreht wird,
durchläuft der H-Pol von D alle Punkte der zu h H-polaren Gerade.

Sei und mit Tripel-Paaren
(s;t) und (u;v) zu Geraden g bzw. h. Dann schneiden sich g und h genau dann, wenn
gg((s;t);(u;v)) = 0 gilt; und die beiden Geraden sind H-orthogonal, wenn zusätzlich
fg((s;t);(u;v)) = 0 ist.

Wenn wir also ein inneres Produkt definieren, dann sind
Geraden zu den Paaren (s;t) und (u;v) genau dann H-orthogonal, wenn das innere Produkt
ist. Jede Tangente von QH ist zu sich selbst H-orthogonal, also auch jede Regulus-Gerade, da sie auch eine
Tangente von QH ist. Ein Tripel-Paar von Gx(r) bzw. Gy(s) ist mit den für Hyp(r;s) benutzten Abkürzungen
und gleich


bzw.
.
Jede Gerade Gx(r) ist zu jeder Geraden Gy(s) H-orthogonal. Das innere Produkt der Tripel-Paare zu
Gx(r) und Gx(r') ist und das der Tripel-Paare zu Gy(s) und Gy(s') ist
.