Es lebe die Geometrie!

Tetraeder, die eine Kanten-Kugel haben

Pdf-Datei https://vivat-geo.de/Pdf-Dateien/Tetraeder.pdf

Die Kanten-Kugel eines Tetraeders ABCD ist eine Kugel, die alle sechs Kanten berührt. Das bedeutet,
dass sich die Inkreise der Seiten-Dreiecke mit einer gemeinsamen Kante ebenfalls berühren, nämlich in
dem Punkt P, in dem die Kugel die Kante berührt. Sei zum Beispiel P ein Punkt der gemeinsamen Kante
BC von den Dreiecken ABC und BCD. Die Längen der Strecken AB, BC und CA seien wie üblich mit
c, a bzw. b bezeichnet und die von BC, CD und DB mit a, cs und bs. Die Länge der Strecke zwischen
B und dem Berührpunkt des Inkreises von ABC mit der Kante BC beträgt . Die analoge
Rechnung im Dreieck BCD ergibt . Aus der Gleichheit folgt . Für die beiden
Seiten-Dreiecke mit der gemeinsamen Kante CA ergibt sich entsprechend . ABCD hat also
genau dann eine Kanten-Kugel, wenn diese beiden Gleichungen erfült sind, die Summe der Längen zu allen drei
Gegenkanten-Paaren also gleich ist.

Der Abstand eines Tetraeder-Eckpunkts von den drei Berührpunkten der Kanten-Kugel mit den von diesem
Eckpunkt ausgehenden Kanten sind gleich. Darum liegen diese drei Punkte P, Q und R auf einer Kugel um
den Eckpunkt, die wir 'Ecken-Kugel' nennen. Den Kreis um P, Q und R nennen wir 'Ecken-Kreis'. Der
Mittelpunkt des Ecken-Kreises, der zugehörige Eckpunkt und der Mittelpunkt der Kanten-Kugel liegen
auf einer Geraden senkrecht zur Ebene durch P, Q und R. Der Mittelpunkt der Kanten-Kugel ist außerdem
der Schnittpunkt der drei Ebenen durch P bzw. Q bzw. R, die senkrecht auf den zugehörigen Kanten stehen.
Dies soll in der folgenden Animation gezeigt werden.

Die ersten vier durch Stops geteilte Abschnitte der Animation zeigen den Übergang von einem
Tetraeder ABCD ohne Kanten-Kugel in ein Tetraeder mit Kanten-Kugel. ABCD wird zunächst
so gedreht, dass man senkrecht auf die Seite ABC blickt. Zu jedem Dreieck gibt es eindeutig
bestimmte Kreise um die Eckpunkte, die sich paarweise berühren. Bei ABC sind es die Radien
bei A, bei B und bei C. Dies sind die
Radien der drei gezeichneten Ecken-Kugeln. ABCD wird mit diesen Kugeln so bewegt, dass man
senkrecht auf die Seite ADC blickt. Aus D heraus wächst eine Ecken-Kugel bis sie die Kugel um C
berührt, nicht aber die um A und B. Um auch den Kontakt mit diesen beiden Kugeln zu erzwingen,
werden schließlich bs in und cs in verändert. Bei dieser Veränderung rücken
auf jeder Kante die Berührpunkte der Inkreise von Seiten-Dreiecken zusammen, die diese Kante
gemeinsam haben. Der Radius der Ecken-Kugel zu D ist dann , wobei
. Die baryzentrischen Koordinaten-Quadupel der Inkreis-Zentren zu
den Gegen-Seiten von A, B, C, D sind die Zeilen der Matrix
,
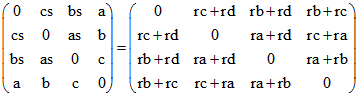die zugehörigen Radien sind , , und .
Die sechs Berührpunkte auf den Kanten AB, BC, CA, DA, DB, DC haben die Quadrupel
(rb;ra;0;0), (0;rc;rb;0), (rc;0;ra;0), (rd;0;0;ra), (0;rd;0;rb), (0;0;rd;rc).

Die anschließenden Stops zeigen ohne Ecken-Kugeln die Inkreise der vier Seiten-Dreiecke, die vier
Ecken-Kreise und die Lote vom Zentrum der Kanten-Kugel auf die Kanten. Zusammen mit der grau
gezeichneten Kanten-Kugel wird ABCD schließlich um 360° gedreht.

Die Quadrupel von den Zentren der Ecken-Kreise lassen sich leider mit den Radien der Eck-Kugeln
nicht einfacher darstellen als mit den Kanten-Längen. Dies gelingt aber bei der Determinante der auf der
vorherigen Seite ' Monge' eingeführte Cayley-Menger-Matrix 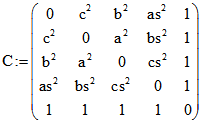, die wegen
der Formel für die Berechnung des Volumens V des Tetraeders bedeutsam ist. Denn es ist
.
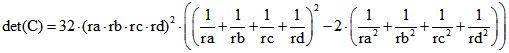Auch die Matrix H, die für die Berechnung der Orthogonalität von Ebenen mit baryzentrischen Koordinaten
benutzt wird, vereinfacht sich:



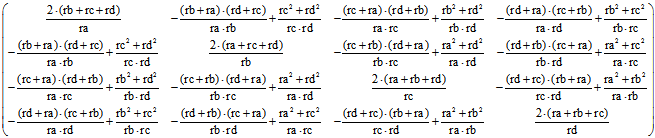
Die Zeilen dieser Matrix sind u-Vektoren senkrecht zu den Seiten-Flächen von ABCD . Nach dem Verfahren,
das am Schluss der vorangehenden Seite ' Monge' beschrieben wurde, kann man die zugehörigen Lot-Geraden
mit Hilfe von Plücker-Koordinaten berechnen. Das Zentrum KZ der Kanten-Kugel ist dann der gemeinsame
Schnitt-Punkt dieser Lot-Geraden. Für Tripel-Paare (s;t) und (u;v) zweier Geraden ergibt sich im Fall des
Schneidens der Punkt zum Quadrupel
. Sie schneiden sich genau dann, wenn , wobei . Für irgend
zwei der vier Lot-Geraden ergibt sich für den Schnittpunkt KZ ein Quadrupel proportional zu
. z ist nicht normiert.
Mit Hilfe des Berührpunktes der Kanten-Kugel mit der Kante AB berechnet man dann den Radius mit
zu .
Wenn man die Geraden durch A, B, C, D und den Punkt zum Quadupel bzw.
mit den Gegen-Seiten von ABCD schneidet, erhält man Dreiecks-Zentren, die
in der Encyclopedia of Triangle Centers (ETC) ( https://faculty.evansville.edu/ck6/encyclopedia/ETC.html)
mit X(7) (Gergonne-Punkt) bzw. X(276) bezeichnet wird. Der Zusammenhang mit dem Kanten-Zentrum
und der Euler-Geraden soll in der folgenden Animation dargestellt werden.

Das erste Bild der Animation zeigt ABCD mit der Kanten-Kugel. Die Lote vom Zentrum KZ auf die
Kanten treffen diese in den Berühr-Punkten. Die Verbindungs-Geraden der Berühr-Punkte auf gegenüber
liegenden Kanten haben den Punkt GZ mit dem Quadrupel gemeinsam. Wir nennen diesen
Punkt Gergonne-Zentrum, weil die Gerade durch GZ und irgendeinen Eck-Punkt das gegenüber liegende
Seiten-Dreieck in dessen Gergonne-Punkt trifft (benannt nach Joseph Gergonne (1771-1859)). Dies ist
der Schnittpunkt der Geraden durch einen Dreiecks-Eckpunkt und dem Berühr-Punkt der gegenüber
liegenden Dreiecks-Seite mit dem Inkreis. Die zugehörigen baryzentrischen Quadrupel ergeben sich aus dem
für GZ, indem man darin eine Komponente durch Null ersetzt. Die Gerade durch KZ und GZ ist parallel zu
der Euler-Geraden, die zusammen mit dem Umkugel-Zentrum (weißer Kern), dem Tetraeder-Schwerpunkt
(schwarz), dem Zwölf-Punkte-Zentrum (grau) und dem Monge-Punkt (magenta) eingezeichnet ist.

Auf der im ersten Bild rot gezeichneten Geraden durch Inkreis-Mittelpunkt IA und Gergonne-Punkt GA liegt
der Schnitt-Punkt KA der Geraden durch A und KZ mit der Seite BCD und das Dreiecks-Zentrum X(279),
das wir mit GqA bezeichnen. GqA hat das Quadrupel und teilt die Strecke von IA
nach GA im Verhältnis . Die Verbindungs-Geraden
der vier Eck-Punkte mit den Punkten GqA, GqB, GqC und GqD treffen sich in dem Punkt GqZ mit dem
Quadrupel auf der Geraden durch KZ und GZ.

Die Geraden durch Eck-Punkte und die Inkreis-Zentren gegenüber liegender Dreieck-Seiten
treffen sich nicht.