Es lebe die Geometrie!

Der Monge-Punkt eines Tetraeders

-->Pdf-Datei https://vivat-geo.de/Pdf-Dateien/Tetraeder.pdf


Unter einem Tetraeder verstehen wir ein Viereck ABCD des dreidimensionalen euklidischen Raums mit
Eckpunkte, die nicht alle in der gleichen Ebene liegen. Die Längen der Kanten des Dreiecks ABC
bezeichnen wir wie üblich mit a, b und c, so dass also a die Länge der Strecke BC ist. Die Längen der
Strecken AD, BD und CD bezeichnen wir mit as (oder a'), bs (oder b') und cs (oder c'). Dies sind die
'Gegen-Kanten' zu a, b bzw. c, weil sie keine gemeinsamen Endpunkte mit AB, BC bzw. CA haben.
Unter der 'Gegen-Seite' eines Eckpunktes verstehen wir das Dreieck aus den drei übrigen Eckpunkten,
zu A also z. B. das Dreieck BDC.

Ähnlich wie für Dreiecke findet man beim Tetraeder ausgezeichnete Punkte, in denen sich besondere Raum-
Geraden treffen, die zu dem Tetraeder definiert werden. Einige Standard-Sätze der Dreiecks-Geometrie
lassen sich dabei direkt übertragen, bei anderen gelingt dies nur unter einschränkenden Voraussetzungen
für das Teraeder. Beim Dreieck treffen sich zum Beispiel die drei Verbindungs-Geraden der Eckpunkte
mit den Mitten der gegenüberliegenden Seiten im Schwerpunkt des Dreiecks. Analog treffen sich die
Verbindungs-Geraden der Eckpunkte jedes Tetraeders mit den Schwerpunkten der Gegen-Seiten im
Schwerpunkt S des Tetraeders.

Anders ist die Lage bei den Raum-Höhen des Tetraeders. Unter einer 'Raum-Höhe' zu z. B. A verstehen wir
die Gerade durch A, die euklidisch orthogonal zur Ebene der Gegen-Seite BDC ist. Während die jeweils
drei 'Flächen-Höhen' in den Seiten-Dreiecken BDC, CDA, ABD und ABC das 'Ortho-Zentrum' des Seiten-
Dreiecks gemeinsam haben, gilt die entsprechende Aussage für die Raum-Höhen nur dann, wenn jeder
Richtungsvektor einer Kanten-Gerade orthogonal zu dem der Gegen-Kante ist. Diese Tetraeder heißen
'orthozentrisch'. Bei einem orthozentrischen Tetraeder ist der Fußpunkt jeder Raum-Höhe das Ortho-Zentrum
der zugehörigen Seiten-Fläche. Bei einem nicht orthozentrischen Tetraeder gilt dies für keinen Fußpunkt. Die
Parallele einer Raum-Höhe durch das Ortho-Zentrum der zugehörigen Seiten-Fläche nennen wir 'Ko-Höhe'.

Der im Folgenden dargestellte Monge-Punkt M fällt für orthozentrische Tetraeder mit dessen Ortho-Zentrum
zusammen, wurde aber durch den Entdecker Gaspard Monge(1746-1818) für beliebige Tetraeder definiert.
M ergibt sich durch Spiegelung des Zentrums der Umkugel von ABCD an dem Schwerpunkt S. Jede Raum-
Höhe hat von M den gleichen Abstand wie die zugehörige Ko-Höhe. Dies soll in der folgenden Animation
dargestellt werden.

Die Animation zeigt den Zusammenhang zwischen dem Monge-Punkt und den Paaren aus parallelen
Höhen und Ko-Höhen. Der Monge-Punkt liegt bei jedem dieser vier Paare auf der Parallelen in der
Mitte dazwischen. Das erste Bild zeigt dies nur für die zur Seite ABC orthogonale Höhe und Ko-Höhe.
In zweiten Bild wird das entsprechende Paar zur Seite BCD hinzugefügt und dann um 360° gedreht.
Diese Seite wird danach durch die Seite DAB ersetzt und diese zuletzt durch die vierte Seite DAC.

Die Gerade durch den Schwerpunkt S und den Mittelpunkt O der Kugel durch die Eckpunkte von
ABCD wird Euler-Gerade genannt. Sie entspricht also beim Dreieck der gleich genannten Geraden
durch das Umkreis-Zentrum und den Dreiecks-Schwerpunkt. Dieser Zusammenhang wird in der
folgenden Animation gezeigt.

Die Euler-Gerade eines Dreiecks inzidiert mit seinem Umkreis-Zentrum, seinem Schwerpunkt und
seinem Ortho-Zentrum. Dabei liegt der Schwerpunkt bei 1/3 des Wegs vom Umkreis-Zentrum zum
Ortho-Zentrum. Der Mittelpunkt zwischen Umkreis-Zentrum und Ortho-Zentrum ist das Zentrum des
Neun-Punkte-Kreises (Feuerbach-Kreises), auf dem die Seiten-Mitten, die Höhen-Fußpunkte und
die Euler-Punkte (Mittel-Punkte zwischen den Eck-Punkten und dem Ortho-Zentrum) liegen. In den
Bildern der Animation sind das Umkreis-Zentrum, der Schwerpunkt, das Neun-Punkte-Zentrum und
das Ortho-Zentrum in dem Dreieck oben links weiß-gefüllt, schwarz, grau bzw.magentafarben
eingezeichnet. Dem entsprechen im Tetraeder ABCD das weiß-gefülltes Umkugel-Zentrum O, der
schwarze Schwerpunkt S, das graue Zentrum N der Zwölf-Punkte-Kugel und der magentafarbene
Monge-Punkt M .

In der Animation wird das Tetraeder ABCD durch Streckungen mit dem Schwerpunkt als Zentrum
abgebildet, und auch das dazu analoge Dreieck oben links. Dabei wandert das weiß-gefüllte
Umkugel-Zentrum Z des Bild-Tetraeders von O nach M. Das im Analogie-Dreieck entsprechende
Umkreis-Zentrum vom Bild-Dreieck bewegt sich dabei bis zum Ortho-Zentrum.. Der Streckungs-Faktor
f wird beginnend bei f = 1 beim Analogie-Dreieck bis -2 und beim Tetraeder bis -1 vermindert. Dabei
ist bemerkenswert, dass sich bei der Euler-Geraden des Tetraeders die Verhätnisse der Abstände
umgedreht haben, denn hier ist S der Mittelpunkt von O und M, und N liegt bei 1/3 des Wegs von M
nach O. Während die Geschwindigkeit von Z konstant ist, bewegt sich darum der weiße Punkt beim
Analogie-Dreieck hinter dem Schwerpunkt mit um die Hälfte vergrößerter Geschwindigkeit.

Z erreicht S für f = 0. Dann ist das Bild-Tetraeder und das Bild-Dreieck zu einem Punkt geschrumpft.
In diesem Zustand werden zu dem Tetreder ABCD die Schwerpunkte der Seiten-Dreiecke angezeigt,
zusammen mit den zugehörigen Verbindungs-Strecken.

Z kommt bei N für f = -1/3 an. Im Analogie-Dreieck wird gleichzeitig das Neun-Punkte-Zentrum für den
Streckungs-Faktor -1/2 erreicht. Dann trifft das Bild-Dreieck mit seinen Eck-Punkten die Seiten-Mitten des
Analogie-Dreiecks und das Bild-Tetreder mit seinen Eck-Punkten die Schwerpunkte der Seiten-Dreiecke.
Die zugehörige Umkugel heißt 'Zwölf-Punkte-Kugel'. Sie wird durch die sechs Groß-Kreise durch jeweils
zwei Eck-Punkte angedeutet. Groß-Kreise durch einen Eckpunkt haben auch das Bild des Eckpunktes bei
Spiegelung an N gemeinsam. Diese Antipoden werden wie beim Dreieck 'Euler-Punkte' genannt. Für jeden
Euler-Punkt von ABCD liegt der Fußpunkt des Lots auf die gegenüberliegende Seiten-Fläche ebenfalls auf
der Zwölf-Punkte-Kugel, so daß sich insgesamt zwölf ausgezeichnete Punkte ergeben, analog zu den neun
ausgezeichneten Punkten des Neun-Punkte-Kreises. Die Fuß-Punkte der Lote von den Euler-Punkten des
Tetraeders entsprechen beim Analogie-Dreieck den Höhen-Fußpunkten.

Das Bild der Zwölf-Punkte-Kugel wird in der Animation um 360° gedreht und anschließend der Punkt Z auf
der Euler-Geraden weiterbewegt, bis er für f = -1 den Monge-Punkt M erreicht. Die Streckung ist dann eine
Punkt-Spiegelung an S, so dass das Bild-Tetreder den gleichen Umkugel-Radius 0,75 wie ABCD hat. M ist
dann also Umkugel-Zentrum des Tetraeders A'B'C'D' , das sich bei Spiegelung von ABCD an S ergibt.
Die Ebene E durch M, die orthogonal zu z. B. A'B' ist, trifft den Mittel-Punkt von A'B', der auch der
Mittel-Punkt von CD ist, da S Mittel-Punkt der Kanten-Mitten gegenüberliegender Kanten ist. E ist
außerdem orthogonal zu AB, da die Spiegelung jede Gerade in eine dazu parallele abbildet.

In der Animation zeigen die letzen fünf Stand-Bilder geometrische Eigenschaften von M. Alle sechs Mittel-
Ebenen des Tetraeeders inzidieren mit M. dabei versteht man unter der 'Mittel-Ebene' z. B. der Kante AB
die Ebene durch den Mittelpunkt von AB, die orthogonal zur Gegen-Kante CD ist. Dies wird zuerst für drei
Ebenen gezeigt, dann für die übrigen drei und schließlich für alle sechs Ebenen zusammen. Die letzten beiden
Standbilder zeigen noch einmal die Euler-Punkte und ihre Lotfuß-Punkte auf der gegenüberliegenden Seiten-
Fläche. Die Euler-Punkte liegen auf 1/3 des Wegs von M zu den Eckpunkten des Tetraeders ABCD .
Analog liegen die Euler-Punkte des Dreieck auf 1/2 des Wegs vom Ortho-Zentrum zu den Eckpunkten.

Zur Berechnung von O, S, N und M in baryzentrischen Koordinaten :

In den vorangehenden Bildern sind die Eckpunkte des Tetraeders ABCD in kartesichen Koordinaten
angegeben, also bei einem Koordinatensystem mit drei Achse, die paarweise euklidisch orthogonal
sind und bei denen die Punkte (1;0;0), (0;1;0) und (0;0;1) den euklidischen Abstand 1 vom Ursprung
(0;0;0) haben. Bei Verwendung von baryzentrischen Koordinaten (Schwerpunkts-Koordinaten) mit dem
Basis-Tetraeder ABCD wird dagegen jeder Punkt P des dreidimensionalen affinen Raums als
Linearkombination mit der Neben-Bedingung dargestellt,
wobei a, b, c und d die kartesischen Koordinaten-Tripel von A, B, C und D sind. Das Quadrupel
ist dann das 'normierte baryzentrische Koordinaten-Quadrupel' zu P. Wenn man es mit einer
Zahl ungleich 1 oder 0 multipliziert, wird es 'unnormiertes' baryzentrische Koordinaten-Quadrupel genannt.
Da zum Beispiel für den Schwerpunkt S von ABCD gilt, ist .
Der Vorteil dieser Koordinaten besteht darin, dass sie wie beim Schwerpunkt zum Teil einfacher sind als
die kartesischen Koordinaten, oder darin, dass damit ausgezeichneten Punkten von ABCD geometrische
Größen zuordnen werden können. Das unnormierte baryzentrische Quadrupel aus den Größen der Seiten-
Flächen von ABCD gehört z. B. zum Inkugel-Zentrum von ABCD. Außerdem: Ein Punkt P liegt genau
dann im Innern von ABCD, wenn seine baryzentischen Koordinaten alle positiv sind.

Die Zahlen r, s, t und u des baryzentrischen Quadrupels haben folgende geometrische
Bedeutung: Wenn die Punkte A und P auf der gleichen Seite der Ebene BCD liegen, ist r der Quotient
aus den Raum-Inhalten der Tetraeder PBCD und ABCD. Wenn A und P von der Ebene BCD getrennt
werden, multipliziert man diesen Quotienten mit -1. Für P auf BCD ist r = 0. Entsprechend betrachtet
man zur Bestimmung von s den Quotienten der Raum-Inhalten der Tetraeder APCD und ABCD. Bei
dieser Deutung ist stets die Summe r+s+t+u gleich 1, auch für P außerhalb von ABCD. Denn wenn
zum Beispiel r negativ ist, aber s, t und u positiv, dann ist die Vereinigungsmenge der Tetraeder APCD,
ABPD und ABCP das Polyeder, das sich aus PBCD und ABCD zusammensetzt.

Die Berechnung der baryzentrische Quadrupel wird folgendermaßen erleichtert: Wir verstehen unter
, , , und die Quadrupel, die sich ergeben, wenn man die kartesischen Koordinaten-Tripel
p, a, b, c und d von P, A, B, C und D um die vierte Koordinate 1 zu einem Quadrupel erweitert. sei
die Basis-Matrix mit den Quadrupeln von A, B, C und D als Zeilen. Dann ist baryzentrisches
Koordinaten-Quadrupel von P. (Dabei dient der tiefgestellte Punkt als Verknüpfungs-Zeichen für die
Matrix-Multiplikation und das Quadrupel wird als Matrix mit nur einer zeile betrachtet.)

Wenn ein Tripel v reeller Zahlen um die vierte Koordinate 0 ergänzt wird, gibt das so entstandene
Quadrupel einen Punkt V der zum affinen Raum gehörenden 'unendlich fernen' Ebene des projektiven
Raums an. Dabei beschreibt jedes Quadrupel den gleichen Punkt, das sich aus durch Multiplikation der
Komponenten mit der gleichen Zahl ungleich Null ergibt. ist dann das zugehörige baryzentrische
Quadrupel. Es ist nicht normierbar, weil die Summe der Komponenten Null ist. Die Menge dieser Quadrupel
bezeichnen wir mit U, weil sie Punkte der unendlich fernen Ebene beschreiben. Die Differenz
zweier normierter baryzentrischer Quadrupel zu affinen Punkten P und Q nennen wir 'u-Vektor' und
bezeichnen sie mit . Wir können es als baryzentrischen Verbindungs-Vektor von P und Q oder als
baryzentrisches Quadrupel des unendlich fernen Punktes auf der Geraden PQ ansehen.


Zu kartesischen Tripeln v und w seien , die zugehörigen u-Vektoren und
die Spalte, die durch Transponieren der Zeile entsteht und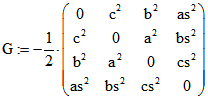
,
wobei a, b, c, as, bs und cs die oben definierten Kantenlängen von ABCD sind.
Dann ist .
Wir definieren darum im Einklang mit dem euklidischen Skalar-Produkt für u-Vektoren .

Unter der 'Umkugel von ABCD ' verstehen wir die Kugel-Fläche, auf der die Eckpunkte A, B, C, D liegen.
Ein Punkt P liegt genau dann auf dieser Umkugel, wenn ist. Für ist dies die
Gleichung .

Wenn p normiertes baryzentrisches Quadrupel eines beliebigen Punktes P des Raums ist, gibt
die Potenz von P zur Umkugel an. Dies ist die Differenz des Quadrates des Abstands des Umkugel-Zentrums
von P und des Quadrats des Radius der Umkugel. Wenn P außerhalb der Kugel liegt, ist die Potenz das
Quadrat des Abstands von P zum Berührpunkt einer beliebigen Tangente von P an die Umkugel; und für
eine Sekante durch P ist die Potenz das Produkt der Abstände der Schnittpunkte der Sekante von P. Wenn
P nicht außerhalb der Kugel liegt, ist die mit -1 multiplizierte Potenz das Produkt der Abstände von P zu den
Endpunkten einer beliebigen Sehne durch P.



Die Cayley-Menger-Matrix 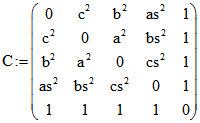wurde vom 20jährigen Arthur Cayley
(1821-1895) zur Berechnung des Volumens eines Tetraeders aus den Kantenlängen
eingeführt, was in anderer Form schon dem Maler Piero della Francesca (ca. 1415-1492) gelungen war.
C ist wie G symmetrisch zur Haupt-Diagonalen von links oben nach rechts unten, in der nur Nullen stehen.




Die ersten vier Komponenten in der fünften Zeile der inversen Matrix von C ergeben das normierte
baryzentrische Quadrupel des Umkugel-Zentrums O und die fünfte ist , wobei R der
Umkugel-Radius ist. Man erkennt, wie aus der 1. Komponente die folgenden entstehen, nämlich an den
Kanten-Längen der Gegen-Seite des i-ten Eckpunkts: .





Die Formel für den Radius zeigt wegen der Form von det(G) eine Ähnlichkeit mit der entsprechenden Formel
für den Umkreis-Radius eines Dreiecks, die sich mit Hilfe der Gleichung von Heron (1. Jahrhundert) ergibt:


Für normierte baryzentrische Punkt-Quadrupel beschreibt die Abbildung die
Streckung mit dem Zentrum S und dem Streckungs-Faktor f . Für und bzw.
ergeben sich die baryzentrischen Quadrupel von N und M, nämlich und .

Es sei die reduzierte Matrix, die entsteht, wenn man bei die letzte Zeile und die letzte Spalte weglässt.
sei die Matrix mit lauter Einsen in der Haupt-Diagonalen und sonst nur Nullen.
Die Matrix hat dann folgende bemerkenswerte Eigenschaften:

H ist wie G symmetrisch zur Haupt-Diagonalen, hat aber anders als G die Determinante Null.
H.G.H = H, also auch .
Alle Zeilen von H sind u-Vektoren.
Für jeden u-Vektor gilt .
Die i-Zeile oder Spalte von H ist euklidisch orthogonal zur i-ten Seiten-Fläche von ABCD.
Die mit berechnete Länge des u-Vektors in der i-ten Zeile von H ist der Kehrwert der
i-ten Höhen-Länge . Das ist der Quotient aus dem Inhalt der i-ten Seitenfläche und dem dreifachen
Tetraeder-Volumen.
Die Komponente in der i-ten Zeile und j-ten Spalte von H ist das Matrix-Produkt .
Dies ist das Produkt aus den Längen von und und dem Kosinus des Winkels dazwischen.

Die i-te Zeile von G.H ist der Verbindungs-Vektor des Umkugel-Zentrums mit dem i-ten Eckpunkt.

Die Komponente in der i-ten Zeile und j-ten Spalte von G.H.G ist .
Dies ist das Produkt des Quadrats vom Radius R der Umkugel mit dem Kosinus des Winkels
zwischen und . In der Haupt-Diagonalen von G.H.G steht also in jeder Zeile .

Um die Komponenten der Matrix H übersichtlich zu beschreiben,
betrachten wir die Tripel der Kantenlängen-Quadrate der i-ten Seitenfläche :
, , , .
Zu jedem dieser Tripel definieren wir vier Typen von Tripel, die
wir mit den Hoch-Zeichen abc, bac, cba und acb markieren:




und anlog für die andern drei Kanten-Tripel. Dann gilt bei
Verwendung des inneren Produkts für euklidische Tripel: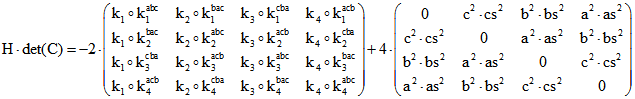



Das kartesische Koordinaten-Quadrupel einer Ebene E im dreidimensionalen
euklidischen Raum setzt sich aus einem Normalen-Vektor senkrecht zu E und einer
vierten Komponente zusammen, die den Abstand vom Ursprung bestimmt. Ein Punkt P inzidiert mit E,
wenn für sein kartesisches Koordinaten-Quadrupel gilt:
.
Baryzentrische Ebenen-Quadrupel berechnet man mit Hilfe der Matrix , die dadurch entsteht,
dass die Basis-Matrix an der Haupt-Diagonalen gespiegelt wird. Es sei nämlich .
Dann inzidiert E mit P genau dann, wenn .

Ebenen D und E sind euklidisch orthogonal, wenn für ihre kartesischen Koordinaten-Quadrupel
d und e gilt: .Das innere Produkt, das sich daraus
für die baryzentrischen Ebenen-Quadrupel ergibt, hat nicht diese einfache Form, erleichtert es aber,
geometrische Bezüge herzustellen. Es ist nämlich . Wenn und Quadrupel mit einer 1
an i-ter bzw. j-ter Stelle und sonst nur Nullen sind, gehören sie zu Seiten-Ebenen von ABCD. Dann
ist . Daraus ergibt sich für
beliebige Ebenen D und E, indem man links und rechts des Gleichheits-Zeichens die gleichen Linear-
Kombinationen bildet. Analog wie bei den u-Vektoren definieren wir darum .

Die Schnittgerade zweier verschiedener Ebenen D und e kann mit kartesischen Plücker-Koordinaten
durch das Tripel-Paar

beschrieben werden und analog (mit vertauschten Tripeln) eine Gerade g durch Punkte P und Q mit den
kartesischen Quadrupeln und durch das Tripel-Paar
.
(--> https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf ).
Wir kürzen dieses Tripel-Paar durch ab. Mit der Plücker-Matrix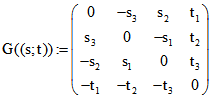
und dem kartesischen Punkt-Quadrupel ergibt dann
das kartesische Ebenen-Quadrupel der Ebene durch X und g, falls X nicht auf g liegt; andernfalls ergibt sich
das Null-Quadrupel. Wenn e kartesisches Quadrupel einer Ebene ist und , ergibt das
Matrix-Produkt ein kartesisches (möglicherweise nicht normiertes) Quadrupel des Schnittpunkts
der Ebene E mit g, falls g nicht auf E liegt; andernfalls ergibt sich das Null-Quadrupel. Die gleichen
Rechnungen sind verwendbar, wenn man von baryzentrischen Ebenen- bzw. Punkt-Koordinaten ausgeht.
Man erhält dann wieder baryzentrische Koordinaten im Ergebnis. Ein Tripel-Paar einer Geraden, das aus
kartesischen bzw. baryzentrischen Quadrupeln errechnet wird, nennen wir 'Tripel-Paar von g in kartesischen
bzw. baryzentrischen Plücker-Koordinaten'. Zur Unterscheidung von kartesischen und baryzentrischen
Koordinaten verwenden wir die Hoch-Zeichen und .

In dem kartesichen Tripel-Paar einer Geraden g ist das Tripel eines Verbindungs-Vektors zweier
Punkte, also kartesisches Quadrupel des unendlich fernen Punktes auf g. ist kartesisches Quadrupel
der Ebene durch g und den affinen Punkt mit dem Tripel (0;0;0),falls g nicht durch diesen Koordinaten-Ursprung
geht. Physikalisch wird als Kraft-Vektor mit g als Wirkungs-Gerade und als zugehöriges Drehmoment
bezüglich des Ursprungs. Für die Tripel des zugehörigen baryzentrischen Tripel-Paars gibt es einen
entsprechenden Zusammenhang nicht.

Zu jedem baryzentrischen Quadrupel eines Punktes V auf der unendlich fernen Ebene [1;1;1;1]
bezeichnen wir die Ebene zum Quadrupel als 'Polar-Ebene zu V' und die Schnitt-Gerade dieser
Ebene mit der Polar-Ebene zu V 'Polar-Gerade' zu V oder zu . Die u-Vektoren, die zu den Punkten
dieser Geraden gehören, sind orthogonal zu . Wenn man Geraden im Raum mit Hilfe von
baryzentrischen Plücker-Koordinaten darstellt, ist die Schnitt-Gerade zu und
[1;1;1;1] die Gerade mit dem Tripel-Paar .
Die zugehörige baryzentrische Plücker-Matrix ist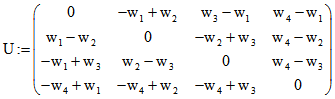

Die zu orthogonale Ebene durch einen Punkt P hat dann das Quadrupel p.U.

Zur Orthogonalität von Geraden g und h zu baryzentrischen Tripel-Paaren und
( Siehe dazu auch die Hinweise am Schluss der Seite ' Ceva'.) Wir definieren: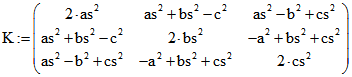













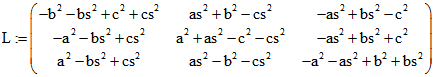
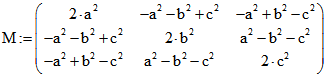
ist äquivalent damit, dass g und h sich schneiden.

ist für jede Gerade g gleich Null.

ist Tripel-Paar einer Geraden in der unendlich fernen Ebene, die wir 'Polare von g' nennen.

g und h schneiden sich genau dann euklidisch orthogonal,
wenn und ist.

Dabei gilt , aber .

Wenn Ebenen A, B sich in g schneiden und C, D in h, dann ist ähnlich wie bei der Lagrange-Identität



Darstellung der Komponenten von G mit denen von H:

Die Darstellung der baryzentrischen Quadrupel zu besonderen Tetraeder-Zentren wie dem Monge-Punkt
kann zum Teil vereinfacht werden, indem man die Komponenten von G durch die von H ersetzt. Dazu
benutzen wir folgende Bezeichnungen: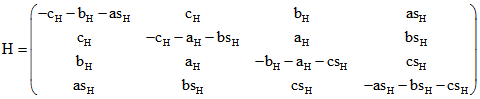


Die Zahl bzw. ist das euklidische Skalarprodukt von Vektoren, die
orthogonal zu Seiten-Flächen des Tetraeders sind, die sich in der Kante mit der Länge as , bs , cs, a , b
bzw. c treffen. Jede Komponente von G ergibt sich als Quotient mit dem gleichen Nenner N und einer
Summe von Produkten von zwei mit H indizerten Zahlen. Die Zahl N ist die Summe aller Produkte von
drei paarweise verschiedenen mit H inzidierten Zahlen mit Ausnahme der Dreier-Produkte
. N ist der Kehrwert von .

Dies ist die Summe aus allen Produkten von zwei mit H indizierten Zahlen ohne mit Ausnahme von
. Analog ergibt sich



Dies ist die Summe aus allen Produkten von zwei mit H indizierten Zahlen ohne mit Ausnahme von
.



Der Monge-Punkt hat das (unnormierte) baryzentrische Koordinaten-Quadrupel



.


.......