Es lebe die Geometrie!
Hauptmenü
- Home
- Geometrie 1
- Geometrie 2
- Epizykeltheorie
Höhen 2
Geometrie 2 > Tetraeder
Raum-Höhen im Tetraeder 2
->Pdf-Datei https://www.vivat-geo.de/Pdf-Dateien/Tetraeder.pdf
Auf dieser Seite wird in der ersten Gleitschau auf Grund des schon auf der vorangehenden Seite ' Höhen 1'
benutzten Vierecks KLMN die rechnerische Erzeugung des Hyperboloids H dargestellt, zu dem die Höhen
des Tetraeders ABCD zu einem Regulus gehören und ihre Ko-Höhen zu dem anderen. Dabei wird für die
Bestimmung der Gleichung für die Punktmenge von H ein anderes Verfahren benutzt als am Schluss der
vorherigen Seite.
Die zweite Gleitschau zeigt den Übergang zu einem orthozentrischen Tetraeder, zu dem es kein Hyperboloid
gibt, da sich die vier Raum-Höhen im Monge-Punkt treffen. Die dritte Gleitschau verdeutlicht die Rolle der
Kubus-Ecken für ein orthozentrisches Tetraeder.
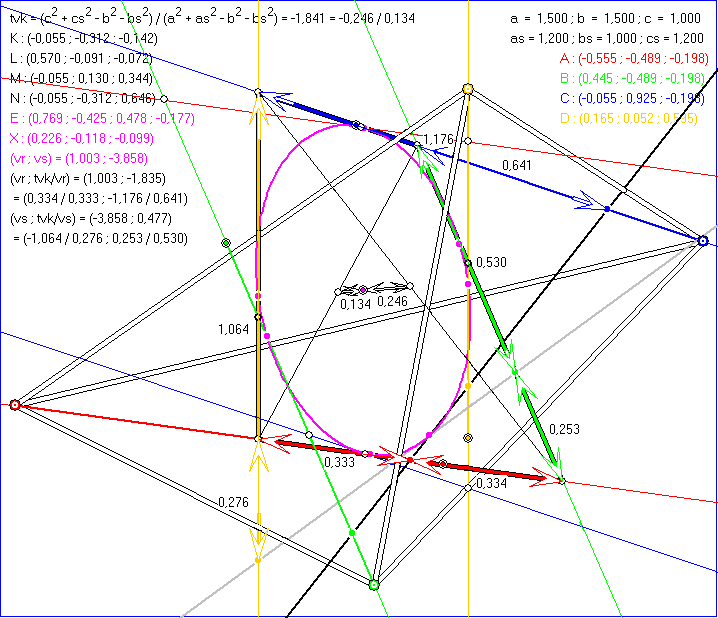





Diese Gleitschau erklärt die Rechnungen, die der Konstruktion des Hyperboloids H in der vorherigen
Seite ' Höhen 1' zugrunde liegen. Wir benutzen das Verfahren auf den Seiten ' Ceva' und ' Hyperboloid 2'.
Das dort benutzte Basis-Viereck ABCD entspricht beim Tetraeder dem schon auf der vorigen Seite
eingeführten Viereck KLMN. Dieses hat Kanten-Geraden, die bei einem Umlauf K-->L-->M-->N-->K
abwechselnd den beiden disjunkten Regulussen angehören. Es ist das Viereck mit Raum-Höhen KL
und MN und zwei Ko-Höhen LM und NK. Das Hyperboloid ist durch dieses Viereck noch nicht
vollständig festgelegt, sondern erst dann, wenn man eine Teilverhältniskonstante tvk bestimmt, die sich
hier durch die Form des Tetraeders ergibt. Es ist nämlich ![]() . Dabei sind die
. Dabei sind die
Terme ![]() ,
, ![]() und
und ![]() die Summen der Quadrate von den Gegenkanten-Längen
die Summen der Quadrate von den Gegenkanten-Längen
![]() ,
, ![]() und
und ![]() . Wenn diese drei Summen
. Wenn diese drei Summen
übereinstimmen, ist das Tetraeder orthozentrisch, das Hyperboloid entartet zu einer Geraden und tvk ist
unbestimmt, da der Nenner Null ist. Andernfalls kann die Punktmenge des Hyperboloids folgendermaßen
beschrieben werden: Wir ergänzen jedes Tripel p = (px;py;pz) eines Punktes P des affinen Raums durch
eine vierte Komponente 1 zu ![]() , um ihn in den projektiven Raum einzubetten. Ein Punkt P
, um ihn in den projektiven Raum einzubetten. Ein Punkt P
gehört genau dann zum Hyperboloid H, wenn gilt:
![]()
Siehe dazu auch die Seite ' Hyperboloid 2'.
Im ersten Bild der Gleitschau zeigt sich tvk in dem Teilverhältnis, in dem der Monge-Punkt M die Strecke
zwischen den Mittelpunkten der Strecken KM und LN teilt. Es ist nämlich gleich -tvk. Die schwarze Gerade
g des Ko-Höhen-Regulusses und die graue Gerade g' des Höhen-Regulusses schneiden sich in dem Punkt X
auf der Ellipse Ell. Das Quadrupel ihrer Ebene E ist (0,769;-0,425;0,478;-0,177). Der Schnittpunkt P von
g mit KL teilt KL im Verhältnis ![]() und der Schnittpunkt Q mit MN teilt MN im Verhältnis
und der Schnittpunkt Q mit MN teilt MN im Verhältnis![]() . Dadurch dass das Produkt dieser Teilverhältnisse gleich tvk ist, wird für jeden
. Dadurch dass das Produkt dieser Teilverhältnisse gleich tvk ist, wird für jeden
Wert von vr erreicht, dass g eine Gerade des Ko-Höhen-Regulusses ist. Für g' gibt es einen analogen
Zusammenhang, wenn man die Reihenfolge der Punkte KLMNK in KNMLK umkehrt: Der Schnittpunkt
R von g' mit dre Geraden KN teilt die gerichtete Strecke KN im Verhältnis ![]() und
und
der Schnittpunkt S mit ML teilt ML im Verhältnis ![]() . Wenn das Produkt der Teilverhältnisse
. Wenn das Produkt der Teilverhältnisse
gleich tvk ist, gehört g' zum Höhen-Regulus, egal wie der Wert von vs gewählt wird. Wenn allerdings g und g'
einen Schnittpunkt X in einer bestimmten Ebene haben sollen, sind vs und vr nicht unabhängig, sondern es
muss ![]() sein, wobei e das kartesische Quadrupel der Ebene ist,
sein, wobei e das kartesische Quadrupel der Ebene ist, ![]() die Spalte der
die Spalte der
Komponenten dieses Quadrupels und der tiefgestellte Punkt für die Matrizen-Multiplikation steht. Wenn g
und g' sich in einem bestimmten Punkt X treffen sollen, sind vr und vs beide dadurch festgelegt.
Wir nennen (vr ; vs) 'H-Koordinaten-Paar' von X. Dabei gilt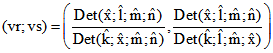 .
.
Alle Punkte einer schwarze Gerade des Ko-Höhen-Regulusses haben den gleichen vr-Wert und alle Punkte
einer grauen Gerade des Höhen-Regulusse haben den gleichen vs-Wert.
Das 2. bis 18. Bild der Gleitschau zeigen die Daten für g und g' bei einem Umlauf von X um die Ellipse in E.
Die darauf folgenden 18 Bilder stellen die gleichen Daten mit einer anderen Ansicht auf die Konstruktion dar.






Diese Animation zeigt den Übergang zu einem orthozentrischen Tetraeder. Das erste Bild zeigt das
Tetraeder ABCD mit den vier Raum-Höhen und den dazu parallelen Ko-Höhen. Im zweiten Bild
werden die Flächen-Höhen der Seite ABC hinzugefügt und im dritten die Kubus-Spitze zu ABC mit
der Eigenschaft, dass alle Kanten des Dreiecks ABC von dieser Kubus-Spitze S aus gesehen unter
einem Winkel der Größe 90° erscheinen. Daraus ergeben sich die Quadrate der Kanten-Längen
![]() ,
, ![]() und
und ![]() deren Wurzeln
deren Wurzeln
oben links im Bild angegeben sind. Wenn f den Flächeninhalt von ABC bezeichnet, ist der Abstand
des Höhen-Fußpunkts von S ist gleich ![]() . Das Quadrupel
. Das Quadrupel ![]() ist
ist
(nicht normiertes) baryzentrisches Quadrupel des Orthozentrums von ABC .
Im vierten Bild werden die drei Geraden zugefügt, die orthogonal zu gegenüber liegenden Tetraeder-
Kanten sind. Sie schneiden sich bei diesem Tetreder nicht. Anschließend werden die Kantenlängen
a und cs so verändert, dass die Ellipse kleiner wird und im Grenzfall in den Monge-Punkt übergeht.
Dann stimmen die Summen von den Quadraten der Gegenkanten-Längen oben links im Bild überein.
Außerdem schneiden sich dann die drei Orthogonalen der Gegenkante im Monge-Punkt.
Diese Konstruktion wird dann um 360° gedreht. Dabei sind Stopps eingefügt, die zeigen, dass die
Gegenkanten zueinander orthogonale Richtungs-Vektoren haben.





Diese Animation schließt an die Konstruktion der vorherigen an. Die ersten drei Bilder zeigen die Kubus-Spitzen
von BCD , ACD und ABD getrennt, und das vierte alle vier Kubus-Spitzen des orthozentrischen Tetraeders
zusammen. Dabei zeigt sich, dass jeder Eckpunkt von den drei Kubus-Spitze den gleichen Abstand hat, die nicht
mit dem Eckpunkt auf einer Raum-Höhe liegen. Diese liegen also gemeinsam auf einer Kugelfläche mit dem
Eckpunkt als Zentrum. Das wird im fünften Bild durch Kreisbögen ausgedrückt. Die entstehende Figur wird
um 360° gedreht.
Zur Berechnung der Daten eines orthozentrischen Tetraeders ABCD :
Es sei ![]() . Wir bezeichnen den Radius der Kugelfläche durch drei
. Wir bezeichnen den Radius der Kugelfläche durch drei
Kubus-Spitzen mit dem Zentrum A bzw. B bzw. C bzw. D mit ra, rb, rc und rd. Dann ist ![]() .
.
Die Größen der Seiten-Flächen seien mit fa, fb, fc und fd bezeichnet. Dann ist![]() ,
, ![]() ,
,![]() ,
, ![]()
Die Abstände der vier Kubus-Spitzen von ihren Grundseiten sind dann gegeben durch das Quadrupel![]() .
.
Das Volumen des Tetraeders ist ![]() .
.
Der Monge-Punkt, in dem sich hier die Höhen schneiden, hat das nicht normierten baryzentrischen Quadupel![]() .
.
Die Höhen-Fußpunkte haben also die nicht normierte baryzentrische Quadupel![]() ,
,![]() ,
, ![]() und
und ![]() .
.
Die Kubus-Spitze zur Gegen-Seite von A hat das nicht normierte baryzentrische Quadupel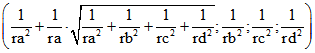 , für die anderen Spitzen zählt man zyklisch weiter
, für die anderen Spitzen zählt man zyklisch weiter
nach dem Schema ra --> rb --> rc --> rd --> ra.
Die nach der Seite ' Monge' für die Maß-Bestimmung mit baryzentrischen Quadrupel benötigten Matrizen
G und H lassen sich mit ra, rb, rc und rd folgendermaßen ausdrücken: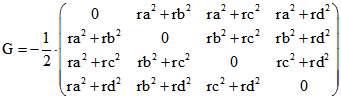
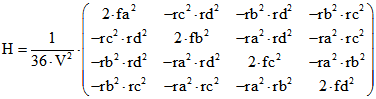
Untermenü