Es lebe die Geometrie!

Pedales und antipedales Tetraeder

Zu einem Testpunkt X des dreidimensionalen Raumes und einem Tetraeder ABCD definieren wir das dazu
gehörige 'pedale' Tetraeder , wobei , , bzw. der Fußpunkt (pedal-point)
des Lots von X auf die Ebene der Gegen-Seite von A, B, C bzw. D im Tetraeder ABCD ist. ist also der
Schnittpunkt der Ebene BCD mit der Geraden g durch X, die euklidisch orthogonal zu dieser Ebene ist.

, bzw. sei die Ebene durch B, C bzw. D , die euklidisch orthogonal zur Geraden XB, XC
bzw. XD ist, und der gemeinsame Punkt dieser drei Ebenen. heißt 'antipedaler' Punkt zu X
bezüglich ABCD. Wenn X auf einer Kante von ABCD liegt, ist es ein unendlich ferner Punkt. Das zu ABCD
gehörige 'antipedale' Tetraeder ist das Tetraeder .
Es heißt 'antipedal', weil ABCD das zu pedale Tetraeder ist.

Auf dieser Seite soll der geometrische Zusammenhang zwischen dem pedalen und dem antipedalen
Tetraeder von ABCD dargestellt werden.

Das erste Bild dieser Animation zeigt zum Tetraeder ABCD das pedale Tetraeder mit
dem Lot . Da die zweite baryzentische Koordinate von X negativ ist, liegt X außerhalb von ABCD .
Der Fuß-Punkt ist mit einem roten Dteieck eingerahmt, das die gleiche Form wie das Dreieck BCD
hat, in dessen Ebene dieser Fuß-Punkt liegt.

Die entsprechende Zeichnung für den zweidimensionalen Raum unten rechts im Bild zeigt das pedale Dreieck
von einem Testpunkt X zum Dreieck ABC. Die Koordinaten dieser Punkte unterscheiden sich von denen der
Punkte im Tetraeder. Um die Analogie zwischen dem zwei- und dem dreidimensionalen Fall deutlicher zu
machen, liegt X außerhalb von ABC.

Nach der Ergänzung durch die Lote , und wird ABCD um 360° gedreht. In gleicher
Art wird anschließend mit dem antipedalen Tetraeder verfahren, ohne das pedale Tetraeder zu zeigen.
Ein Standbild macht dann einen wichtigen Zusammenhang zwischen beiden Tetraedern deutlich. Dabei
spielt das Zentrum O der Umkugel von ABCD eine zentrale Rolle. Er ist als doppelt umrandeter Punkt
mit weißem Kern eingezeichnet. Die zeitweise mit Doppel-Pfeil und Zahl markierten Strecken zeigen:
Die Fußpunkte und von O und dem antipedalen Punkt auf die Ebene
BCD und der pedale Punkt liegen auf einer Geraden mit in der Mitte
zwischen den anderen beiden Punkten. Dies gilt entsprechend für B, C und D.

Die drei Tetraeder werden mit den Loten zu A und D um 360° gedreht. Dabei sind die Fußpunkte
der antipedalen Punkte mit Dreiecken in der Form des zugehörigen Seiten-Dreiecks markiert mit
jeweils drei grauen Orthogonalitäts-Zeichen. Den gleichen geometrischen Zusammenhang zeigt die
zweidimensionale Figur unten rechts.

Im letzten Teil der Animation wird ein viertes Tetraeder zugefügt, das sich
durch Verschiebung des antipedalen Tetraeders mit dem doppelten Verschiebungs-Pfeil von O nach X
ergibt. Es zeigt sich, dass die Punkte , X und kollinear sind. Dies erschließt sich daraus, dass
die Geraden und Parallelen im Raum sind mit als Gerade in der Mitte
dazwischen, so dass der Punkt Y, der sich durch Spiegelung von X an O ergibt, auf liegt.

Durch diese Animation soll dargestellt werden, dass das verschobene Tetraeder
sich aus dem pedalen Tetraeder durch Verkettung einer Spiegelung an X und der Spiegelung
an der Kugel L um X ergibt, die euklidisch orthogonal zur Umkugel K von ABCD ist.

Das erste Bild zeigt den schwarzen Schnitt-Kreis von K und einer Ebene E durch O und X und den
magentafarbenen Schnitt-Kreis von E mit L. Diese Kreise schneiden sich orthogonal. Durch die
Schnittpunkte verläuft der dünn gezeichnete Schnitt-Kreis von K und L. Er trifft senkrecht auf die beiden
anderen Kreise. Im zweiten Bild werden die beiden Kugeln dargestellt und dann um 360° gedreht. Eine
Vergrößerung zeigt dann die Maße für die Entfernung der Punkte und von X. Das Produkt
dieser beiden Längen stimmt mit dem Quadrat des Radius von L überein. Dies gilt auch dann, wenn man
A durch die anderen Eckpunkte von ABCD ersetzt. Da hier und auf verschiedenen Seiten von
X liegen, folgt daraus, dass sich durch Verkettung der Spiegelung
an X und der Spiegelung an L aus dem pedalen Tetraeder ergibt.

Das antipedale Tetraeder ist darum das Bild des pedalen Tetraeders bei Verkettung
der Spiegelungen an L und O, denn ist die Verschiebung mit dem
doppelten Verschiebungs-Pfeil von X nach O..

Der entsprechende Zusammenhang zeigt sich auch in der zweidimensionalen Figur unten rechts.

Die Animation zeigt, wie sich die Bewegung des Testpunktes X ins Innere des Tetraeders ABCD auf
das pedale Tetraeder und das Verschiebungs-Bild
des antipedalen Tetraeders auswirkt.

X liegt zunächst außerhalb der Umkugel K von ABCD . Das schwarz gezeichnete Projektions-Bild eines
Kreises gehört zum Schnitt-Kreis von K mit einer Ebene E durch das Zentrum von O und X. Das magenta
gezeichnete Projektions-Bild eines Kreises gehört zum Schnitt-Kreis von E mit der Kugel L um X, welcher
K orthogonal schneidet. Die Radien dieser Kreise seien rk und rl. Wegen der Orthogonalität von K und L
sind auch die Schnitt-Kreise orthogonal und für den Abstand dox von O und X gilt .

X wird in Richtung von B bewegt und der entsprechende Punkt in der zweidimensionalen Figur unten rechts in
Richtung A. Wenn X die Kugel-Fläche K erreicht, fallen alle Eckpunkte von Tvap mit X zusammen und alle
Eckpunkte von Tap mit dem Bild Y von X bei Spiegelung an O. Dann ist rl = 0. Analoges gilt auch für die
zweidimensionale Figur.

Wenn sich X weiter ins Innere von K bewegt, wird rl wieder größer. Dann schneiden sich K und L (und auch die
Kreise) nicht mehr orthogonal, denn dann gilt statt der Formel die Gleichung .
In dem rechtwinkligen Dreieck aus O, X und dem Schnittpunkt der beiden Kreise hat der rechte Winkel jetzt
also seinen Scheitel bei X.

Wenn sich X der Seitenfläche ACD nähert, entfernt sich immer mehr und wird bei Erreichen dieser Fläche
ein unendlich ferner Punkt. Nach Verkleinerung der Figur bewegt sich X weiter ins Innere von ABCD . Dabei
hat die Seite von ACD gewechselt, so dass nun Tp im Innern von Tap liegt. Es gilt weiterhin die Gleichung
.

Nach einer 360^-Drehung wird die Figur wieder vergrößert und im letzten Bild an Hand der Abstände der
Punkte und von X gezeigt, dass das Produkt dieser Längen mit dem Quadrat von rl übereinstimmt.
Da X nicht mehr zwischen und liegt, gehen diese Punkte durch eine Spiegelung an L auseinander
hervor. Man braucht also nicht mehr eine Verkettung der Spiegelung an X und an L, wie sie für die Lage von
X außerhalb von K benutzt wurde.

Da bedeutet für X im Innern von K, dass sich Tap aus Tp durch Verkettung der Spiegelungen
an L, X und O ergibt.

Diese Animation zeigt, dass eine geeignete Streckung das antipedalen Tetraeder Tap von ABCD in
ein Tetraeder Tap1 abbildet, dessen Seitenflächen parallel zu denen von Tap sind, die aber alle den
gleichen Abstand 1 von X haben. Die Seitenflächen von Tap1 berühren also eine Kugel um X mit dem
Radius 1. Die Berühr-Punkte von Tap1 bilden ein Tetraeder T1, dessen Eck-Punkte A1, B1, C1 und
D1 von X den Abstand 1 haben und auf der Verbindungs-Geraden von X mit A, B, C bzw. D liegen.
Wir nennen T1 'Einheits-Eck von X zu ABCD'. Dabei kann ein Eck-Punkt von A1B1C1D1 auf der
gleichen Seite von X wie der zugeordneten Eck-Punkt von ABCD liegen, oder auch nicht. Die Zahl
gibt im ersten Fall den Abstand des Punktes X von A an, im zweiten Fall multiplizieren wir diesen
Abstand mit -1. Entsprechend verfahren wir mit den anderen Eck-Punkten. Da man für jeden der vier
Eck-Punkte diese beiden Möglichkeiten hat, gibt es acht Einheits-Tetraeder von X zu ABCD.

Das Zentrum X1 der Streckung, die Tap in Tap1 abbildet, kann man mit kartesischen Koordinaten
folgendermaßen berechnen: Es sei zunächst angenommen, dass X im Ursprung liegt, also das Tripel
(0;0,0) hat. Das Tripel von A sei . Dann hat die Tangential-Ebene an die Einheits-Kugel
um X mit dem Berühr-Punkt A1 das kartesische Quadrupel 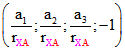. Ein Punkt mit dem
Tripel liegt also genau dann auf dieser Ebene, wenn gilt.
M sei die Matrix mit diesem Quadupel in der ersten Zeile und den entsprechenden Quadrupeln zu B1, C1
und D1 in den anderen Zeilen. sei die Matrix, die entsteht, wenn man M zunächst an der Haupt-
Diagonalen spiegelt und das Ergebnis dann invertiert. Dann ist
ein unnormiertes Quadupel des Streckungs-Zentrums X1 . Das zugehörige Tripel erhält man, indem man
die ersten drei Zahlen des Quadupels durch die vierte Zahl teilt. Um das Streckungs-Zentrum für ein
beliebiges X zu erhalten, verschiebt man ABCD zunächst in den Ursprung und schiebt nach der Rechnung
wieder zurück. Es wird also in der Matrix M von den Tripeln zu A, B, C und D das Tripel von X subtrahiert,
so dass in der ersten Zeile der geänderten Matrix M' das Quadrupel 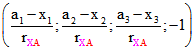steht.
Das Tripel von X1 ergibt sich, wenn man die ersten drei Komponenten des Quadupels durch die vierte teilt und dazu , bzw. addiert.

Zur Berechnung des Streckungs-Faktors ersetzen wir in der Matrix M' die vierte Spalte durch
und nennen das Ergebnis N'. Der Streckungs-Faktor ist der Betrag des
Quotienten der Determinanten von M' und N'. Der in der Animation angegebene Streckungsfaktor
gehört zu der Streckung, die Tap1 in Tap abbildet.

Zur Berechnung des pedalen und des antipedalen Tetraeders mit baryzentrischen Koordinaten

Wir beschreiben Raum-Geraden mit baryzentrischen Koordinaten analog wie für kartesische Koordinaten.
Die Gerade durch verschiedene Punkte P und Q mit den Koordinaten-Quadrupeln und
berechnet man mit dem Tripel-Paar
und die Schnitt-Gerade zweier verschiedener Ebenen D und E mit dem Tripel-Paar
.
Zu einem Tripel-Paar (s,t) definieren wir die Matrix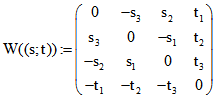 und verstehen unter
die Matrix W((t;s)) mit vertauschtem Tripel-Paar. Das hochgestellte 'd' steht für 'dual'. Dann ist
baryzentrisches Quadrupel der Ebene durch P und die Schnitt-Gerade von D und E, falls
diese eindeuig bestmmt ist; andernfalls ist das Null-Quadrupel aus lauter Nullen und P liegt
auf der Schnitt-Geraden. Analog ist Quadrupel des Schnitt-Punktes
der Geraden PQ mit D, falls dieser eindeutig bestimmt ist; andernfalls ergibt sich das Null-Quadrupel und PQ
verläuft ganz in D.

Die Lot-Gerade durch einen Punkt P senkrecht zu einer Ebene D ist die Gerade durch P und den Pol von D
auf der unendlich fernen Ebene. Die Pole der Seiten-Ebenen von ABCD sind durch die Zeilen der auf der
Seite ' Monge' eingeführten Matrix H gegeben, nämlich 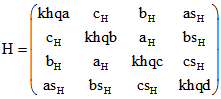mit
.
Das 6-Tupel legt wie das 6-Tupel (a;b,c;as;bs;cs) die Form und Größe von
ABCD fest. (Wir unterscheiden hier die schwarz bezeichnete Ebene D von dem gelb bezeichneten Punkt D.)
Die Umrechnungen werden auf der Seite ' Monge' beschrieben. khqa ist der Kehrwert der Höhen-Länge
zu A zum Quadrat. Wenn P der Test-Punkt X in den Animationen ist, D die Ebene der Gegen-Seite von A
mit dem Quadrupel [1;0;0;0] und die erste Zeile von H, dann ist Quadrupel des
Fußpunkts der Lots von X auf D, also des ersten Eckpunkts des pedalen Tetraeders zu ABCD.

Die vier Quadrupel der Eck-Punkte des pedalen Tetraeders von ABCD ergeben nach dieser Rechnung

die Matrix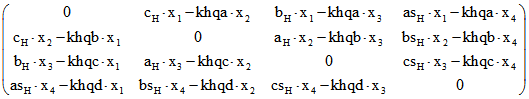

Das 6-Tupel der Quadrate der Kanten-Längen des pedalen Tetraeders ist dann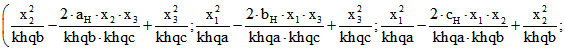


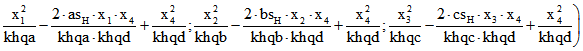
Dabei ist vorausgesetzt, dass x normiert ist, also gilt.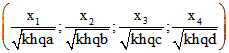
ist hier das Quadrupel der Abstände des Testpunktes X von
den Seiten-Ebenen des Tetraeders ABCD . Man erkennt in den Komponenten des 6-Tupels den
Kosinus-Satz.

Zur Berechnung des antipedalen Tetraeders müssen die Ebenen durch die Eckpunkte von ABCD berechnet
werden, die orthogonal zur Verbindung des Eckpunkts mit X sind. Wir verwenden dazu die auf der Seite
' Monge' eingeführte Matrix 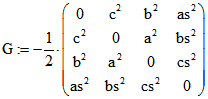, die eine entsprechende Rolle für Punkte spielt
wie H für Ebenen. Wenn d Quadrupel einer Ebene ist, dann ist d.H der unendlich ferne Pol dieser Ebene.
Wenn u Quadrupel eines unendlich fernen Punktes ist, dann ist u.G Quadrupel einer dazu polaren Ebene.
u kann nicht nur als Quadrupel eines Punktes gedeutet werden, sondern auch als Vektor, der senkrecht zur
polaren Ebene steht. Jede dazu parallele Ebene hat die gleiche Schnitt-Gerade mit der unendlich fernen
Ebene mit dem Quadrupel {[1;1;1;1]. Sei zum Beispiel u das Quadrupel des Schnittpunkts der Geraden
XA mit der unendlich fernen Ebene, also die Differenz der Quadrupel von X und A in normierter Form.
Dann ist Tripel-Paar der unendlich fernen Gerade, die auf allen Ebenen
liegt, die zu u orthogonal sind. Darum ist Quadrupel der
zu XA senkrechte Ebene durch A. Man errechnet dafür




Der Schnittpunkt von jeweils drei der vier Ebenen durch einen Eckpunkt von ABCD senkrecht zur Verbindung
des Eckpunkts mit X ergibt dann einen Eckpunkt des antipedalen Tetraeders. Das Quadrupel des Schnittpunkts
von drei Ebenen D, E und F kann man mit berechnen.

Das Ergebnis der Berechnung eines Eck-Punktes vom antipedalen Tetraeder ist ein umfangreicher Term.
Das 6-Tupel der Quadrate der Kanten-Längen des antipedalen Tetraeders hat aber dennoch eine
einfache Form, nämlich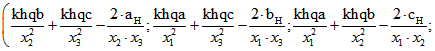


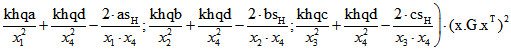
Dabei ist auch hier vorausgesetzt, dass x normiert ist. ist dabei gleich und in den Komponenten
erkennt man auch hier den Kosinus-Satz.

Das Volumen des Tetraeders ABCD sei V genannt. In dem 6-Tupel der Quadrate der Kanten-Längen
des antipedalen Tetraeders von ABCD zu x ersetzen wir durch
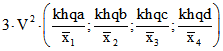. Dabei ist zum Beispiel das Quadrat des
Flächeninhalts der Gegenseite des Eckpunkts A. Dann ergibt sich das 6-Tupel

,
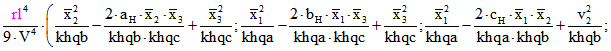
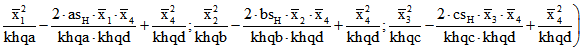das proportional zu dem 6-Tupel des pedalen Tetraeders von ABCD zu ist. Der zum Quadrupel
gehörige Punkt ist der zu X isogonal konjugierte Punkt bezüglich ABCD .



.