Es lebe die Geometrie!

Archimedische Kachelungen

Unter einer archimedischen Kachelung (Parkettierung) versteht man eine Überdeckung der Ebene mit
regelmäßigen nicht sternförmigen Polygonen ohne Überlappungen, bei der an jedem Eckpunkt gleich
viele Polygone in der gleichen Anordnung zusammentreffen. Dabei können die Eckenzahlen der Polygone
unterschiedlich sein. Die Bedingung 'gleiche Anordnung' bedeutet: Wenn die Eckenzahlen der
an einem Eckpunkt der Kachelung zusammentreffenden Polygone sind und die Reihenfolge sich bei einem
Umlauf im oder gegen den Uhrzeigersinn ergibt, dann tritt diese Reihenfolge auch an jedem anderen Punkt
der Kachelung auf, an dem Kacheln zusammentreffen. Reihenfolgen, die durch zyklische Permutation oder
durch Umkehr entstehen, werden dabei nicht unterschieden. Es gibt 11 dieser 'Eck-Charakteristiken' bei
archimedischen Kachelungen, nämlich 3 3 3 3 3 3, 4 4 4 4, 6 6 6, 3 3 3 3 6, 3 3 3 4 4, 3 3 4 3 4,
3 4 6 3, 3 6 3 6, 3 12 12, 4 6 12 und 4 8 8.

Diese Kachelungen werden 'archimedisch' genannt, weil sie Kachelungen der Kugel (statt der euklidischen
Ebene) entsprechen, die mit den archimedischen Körpern zusammenhängen, die nach Aussagen von antiken
Mathematikern zuerst von Archimedes (-287 bis -212) beschrieben worden sind. Siehe dazu die Seite
' Archimedes 1'.

Analog wie dort die archimedischen Körper aus Großkreis-Kachelungen abgeleitet werden, sollen auf
dieser Seite die euklidischen archimedischen Kachelungen mit Kachelungen konstruiert werden, die durch
Nachbarbewegungen erzeugt werden. Dazu wird in einer Kachel ein Punkt P festgelegt, der zu allen
entsprechenden Punkten der Nachbar-Kacheln den gleichen Abstand hat. 'Entsprechend' nennen wir
dabei Punkte, die durch eine Nachbar-Bewegung oder eine Hintereinanderschaltung von derartigen
Abbildungen auseinander hervorgehen. Verbindet man jeden P entsprechenden Punkt mit den analogen
Punkten auf Nachbarkacheln, dann ergeben sich bei Ausgangskachelungen mit gewissen Signaturen auf
diese Weise archimedische Kachelungen. Die P entsprechenden Punkte werden in den folgenden
Animationen gelb markiert. P selbst wird durch einen weißen Rand hervorgehoben.

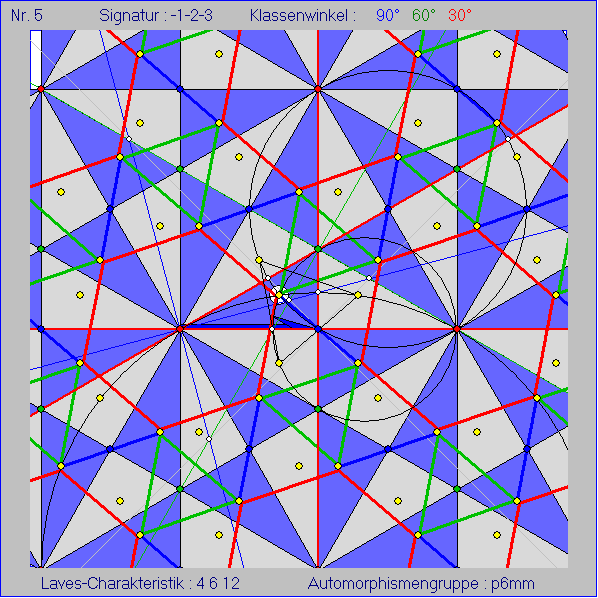
In dieser Animation hat die Ausgangskachelung die Signatur -1-2-3. Die Dreiecke mit den Innenwinkeln
90°, 60° und 30° werden also an den Seiten gespiegelt, um zu den Nachbar-Kacheln zu kommen. Der
mit einem weißen Rand markierte gelbe Punkt P durchläuft einen Weg im Dreieck ABC mit Stopps an
folgenden Punkten:

1. Eckpunkt A
2. Schnittpunkt der Winkelhalbierenden des Winkels ACB mit der Seite AB
3. Eckpunkt B
4. Schnittpunkt der Winkelhalbierenden des Winkels BAC mit der Seite BC
5. Eckpunkt C
6. Schnittpunkt der Winkelhalbierenden des Winkels CBA mit der Seite CA
7. Inkreis-Mittelpunkt M

Wenn P diese Punkte erreicht, bilden die gelben Punkte mit ihren Verbindungen archimedische Kachelungen
mit den Eck-Charakteristiken 3 6 3 6, 3 12 12, 6 6 6, 3 4 6 3, 3 3 3 3 3 3, 6 6 6 und 4 6 12. In den
Positionen dazwischen haben die abgeleiteten Kachelungen mit den gelben Punkten als Ecken zwar Kacheln
mit lauter gleichen Innenwinkeln, aber nicht mit gleichen Seitenlängen.

Die besondere Rolle der Winkelhalbierenden hat hier folgenden Grund: Wenn der Punkt P zum Beispiel auf
der Winkelhalbierenden des Winkels CBA liegt, dann stimmen seine Abstände von den Geraden CB und BA
überein und darum sind die Abstände von den Bildern bei Spiegelung an diesen Geraden ebenfalls gleich. Wir
nennen darum die Winkelhalbierende 'Äquidistanzkurve' der beiden Achsenspiegelungen und erweitern diese
Begriffsbildung im Folgenden auf andere Paare von Nachbarbewegungen.

Der hier dargestellte Weg entspricht dem auf der Seite ' Archimedes 3'. Anstatt einer euklidischen Kachelung
mit 90°-60°-30°-Dreiecken wird dort als Ausgangs-Kachelung eine Großkreis-Kachelung auf der Kugel mit
90°-60°-36°-Dreiecken benutzt, die dort als 'Ikosaeder-Kachelung' bezeichnet wird.

Die Gleitschau im Anschluss an die Animation zeigt Standbilder zu den Positionen, die zu archimedischen
Kachelungen führen.

Bei unveränderter Signatur wurde in dieser Animation das 90°-60°-30°-Dreieck durch ein Dreieck
mit den Innenwinkeln 45°, 90° und 45° ersetzt. Es ergeben sich in den ausgezeichneten Positionen
archimedische Kachelungen mit den Eck-Charakteristiken 4 4 4 4, 4 8 8, 4 4 4 4, 4 8 8, 4 4 4 4,
4 4 4 4 und 4 8 8 . Auf der Kugel entspricht dies den abgeleiteten Kachelungen zur Würfel-Kachelung
auf der Seite ' Archimedes 2', bei der von einem 45°-90°-60°-Dreieck aus Großkreis-Bögen
ausgegangen wird.

Wenn man von einer Kachelung mit gleichseitigen Dreiecken ausgeht, ergeben sich in den ausgezeichneten
Positionen des gelben Punkts archimedische Kachelungen mit den Eck-Charakteristiken 6 6 6 6 6 6 ,
3 6 3 6, 6 6 6 6 6 6 , 3 6 3 6, 6 6 6 6 6 6 , 3 6 3 6 und 6 6 6. Auf der Kugel entspricht dies
den abgeleiteten Kachelungen der Tetraeder-Kachelung auf der Seite ' Archimedes 1', die aus
Kreisbogen-Dreiecken mit den Innenwinkeln 60°, 90° und 60° besteht.

Das erste Bild der Gleitschau zeigt die archimedische Kachelung mit der Eck-Charakteristik
3 3 3 3 6 und ihren Zusammenhang mit der Kachelung, die aus einem 90°-60°-30°-Dreieck durch
Spiegelungen an den Seiten erzeugt wird. Anders als in den vorangegangenen Animationen werden
hier die gelben Punkte nicht mit den entsprechenden Punkten der Nachbar-Kacheln verbunden,
sondern mit denen in der übernächsten Kachel, die sich durch Hintereinanderschaltung zweier
Spiegelungen an Seitengeraden ergibt. Es werden also nur die gelben Punkte in den blau gezeichneten
Dreiecken verbunden, die durch eine gerade Bewegung auseinander hervorgehen und folglich alle
positiv orientiert sind. Damit eine archimedische Kachelung entsteht, muss der mit weißem Ring
markierte gelbe Punkt P im Ausgangsdreieck von allen mit ihm verbundenen gelben Punkten Q den
gleichen Abstand haben. Jeder dieser Punkte Q ergibt sich aus P durch Drehung um einen der
Eckpunkte des Ausgangs-Dreiecks ABC mit dem Drehwinkel, der durch Verdopplung des
Innenwinkels bei diesem Drehpunkt entsteht. Der so definierte Punkt existiert zu jedem Dreieck.
Er heißt '1. isodynamischer Punkt' und wird in der ' Encyclopedia of triangle centers' mit X(15)
bezeichnet. Man konstruiert ihn z.B. als Schnittpunkt der drei Apollonius-Kreise von ABC . Der
A-Apollonius-Kreis ist der Thales-Kreis über den Schnittpunkte der Winkelhalbierenden durch A mit
der gegenüberliegenden Seitengeraden BC. Da sich die Winkelhalbierenden in A senkrecht schneiden,
liegt A auf diesem Kreis. Entsprechendes gilt für B und C. Auf den drei Apollonius-Kreise liegt auch
der 2. isodynamische Punkt X(16). Wenn man den 1. isodynamischen Punkt an den Seitengeraden
spiegelt, entsteht ein gleichseitiges Dreieck. Diese geometrischen Zusammenhänge sind im Bild 5 der
Gleitschau vergrößert dargestellt. Die analoge Konstruktion bei Großkreis-Kachelungen der Kugel
führt bei der Ikosaeder-Kachelung zu dem abgeplatteten Dodekaeder (Dodecaedron simum), der ein
archimedischer Körper ist. Siehe die Seite ' Archimedes 4'.

Begründung dafür, dass P auf den Apollonius-Kreisen liegen muss:

seien die Innenwinkel des Ausgangsdreiecks bei A, B und C und a, b und c die Längen der
gegenüberliegenden Seiten. Da die Bilder von P bei Drehung um B mit dem Drehwinkel und um
C mit dem Drehwinkel den gleichen Abstand von P haben, gilt . Wenn
man beide Seiten mit multipliziert, ergibt sich . Erfüllt ein
Punkt Q(x;y) die Gleichung , dann gilt für seine Koordinaten

.
Der geometrische Ort von Q ist darum ein Kreis, der wegen durch A geht.
Er geht auch durch die Schnittpunkte der Winkelhalbierenden durch A mit der Seitengerade BC,
denn diese Punkte teilen die Strecke BC im Verhältnis b:c außen und innen. Darum ist der Kreis
der A-Apollonius-Kreis. Wir nennen diesen Apollonius-Kreis auch 'Äquidistanzkurve' der Drehungen
um B mit dem Drehwinkel und um C mit dem Drehwinkel .


Bild 3 zeigt die archimedische Kachelung, die ersteht, wenn man die gelben Punkte in den negativ
orientierten grauen Dreiecken verbindet. Sie hat die gleiche Eck-Charakteristik wie die in Bild 1,
entsteht aber daraus durch eine Achsenspiegelung, die kein Automorphismus ist, sie also nicht in
sich selbst überführt. Man erkennt dies z.B. daran, wie sechs rote Sechsecke um ein zentrale
Sechseck angeordnet sind.

Bild 7 veranschaulicht die nicht archimedische Kachelung, die bei Verbindung des 1. isodynamischen
Punktes mit den entsprechenden Punkten der Nachbarkacheln entsteht.

Bild 8 zeigt die Ableitung einer archimedischen Kachelung zur Eck-Charakteristik 3 3 3 3 6 aus einer
durch Nachbar-Bewegungen erzeugten Kachelung zur Signatur 21435 mit den Klassenwinkeln
60°, 360° und 120°. Die Ausgangskachel ist hier ein gleichschenkliges Trapez ABCE auf dessen
Basis-Seite der Mittelpunkt D als fünfter Eckpunkt hinzugefügt wurde. Die Basiswinkel haben die
Größe 60°. Die Nachbar-Bewegungen B1, B3 und B5 sind Drehungen um A bzw. C bzw. den
Mittelpunkt M von DE mit den Drehwinkeln 120° bzw. 60° bzw. 180°. Damit der gelbe Punkt P
im Trapez von allen seinen drei Drehungsbildern den gleichen Abstand hat, muss er auf den drei
eingezeichneten Kreisen liegen. Z. B. der rote Kreis kann so konstruiert werden: Man ergänzt die
Strecke AC durch einen Punkt Q zu einem Dreieck, das bei A die Hälfte vom Drehwinkel 120° als
Innenwinkel-Größe hat und bei C die Hälfte von 60°. Der rote Kreis ist dann der Q-Apollonius-Kreis
dieses Dreiecks. (Q kann z.B. gleich E sein.) Bild 9 zeigt den Zusammenhang in Vergrößerung.

In Bild 13 bis 17 wurde der Startpfeil in der Ausgangskachelung um eine Seite verrückt. Es entsteht
dann eine archimedische Kachelung, die (abgesehen von den Farben) ein Achsenspiegelungsbild der
vorherigen Kachelung ist. Die Bilder 18 bis 21 zeigen, dass sich auch bei Variation der Ausgangkachel
die gleiche archimedische Kachelung ableiten lässt, falls die Signatur und die Klassenwinkel gleich bleiben.

In den Bildern 22 bis 29 hat die zugrunde liegende durch Nachbarbewegungen erzeugte Kachelung die
Signatur 2143. Die Ausgangskachel ist ein Drachen ABCD mit den Winkeln 120°, 90°, 60° und 90°.
Wenn der gelbe Punkt P innerhalb dieser Kachel auf dem roten Kreis liegt, kommt in der abgeleiteten
Kachelung nur eine Seitenlänge vor. Die Kacheln sind regelmäßige Sechsecke, regelmäßige Dreiecke
und Rauten. Der Kreis ist der B-Apollonius-Kreis des Dreiecks ABC . Für zwei Orte auf dem Kreis
hat die Raute die Innenwinkel 60° und 120°, so dass sich bei Teilung in zwei gleichseitige Dreiecke
archimedische Kachelungen mit der Eck-Charakteristik 3 3 3 3 6 ergeben. Liegt P auf dem Kreis und
der Symmetrieachse des Drachens, dann ist die abgeleitete Kachelung archimedisch mit der Eck-
Charakteristik 3 4 6 3.

In den Bildern 30 bis 42 zeigen für die archimedische Kachelung mit der Eck-Charakteristik 3 3 4 3 4
die entsprechenden Zusammenhänge wie für die Eck-Charakteristik 3 3 3 3 6 . Die zugrunde liegende
durch Nachbar-Bewegungen erzeugte Kachelung hat in den Bildern 30 bis 35 ein 45°-90°-45°-Dreieck
als Ausgangskachel mit den Spiegelungen an den Seitengeraden als Nachbar-Bewegungen. Sie entspricht
bei den Großkreis-Kachelungen der Kugel der Würfel-Kachelung (siehe die Seiten ' Würfel-Kachelung'
und ' Archimedes 4'). In den Bilder 37 bis 39 wird archimedische Kachelung zur Eck-Charakteristik
3 3 4 3 4 aus der Kachelung mit der Signatur 21435 wie bei der Charakteristik 3 3 3 3 6 abgeleitet, aber
hier mit den Klassenwinkel 90°, 360° und 90°. Die Ausgangskachel ist ein Fünfeck in Form eines Quadrats
mit aufgesetztem rechtwinklig gleichschenkligen Dreieck. Die Bilder 40 bis 42 gehen von der Signatur
2143 mit den Klassenwinkeln 90°, 180° und 90° aus, deren Ableitung eine Kachelung aus Rauten und
Quadrate mit gleichen Seitenlängen liefert. Wenn die Rauten den Innenwinkel 60° haben, entsteht daraus
durch Teilung in zwei gleichseitige Dreiecke die archimedische Kachelung mit der Signatur 3 3 4 3 4.

Die Bilder 43 bis 49 benutzen die durch Achsenspiegelungen erzeugte Ausgangs-Kachelung mit
gleichseitigen Dreiecken. Die oben anfgegebenen Konstruktionen führen aber hier nur zu der
archimedischen Kachelung mit der Eck-Charakteristik 3 3 3 3 3 3.

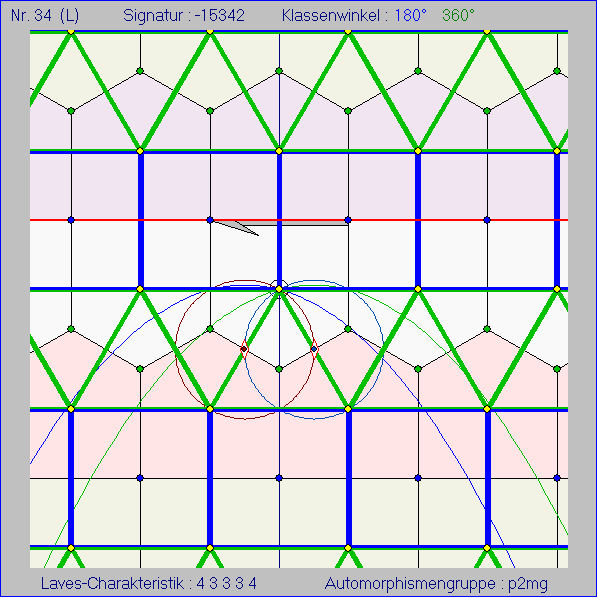
Die Gleitschau stellt die einzige bisher auf dieser Seite noch nicht behandelte archimedische Kachelung
dar, nämlich die mit der Eck-Charakteristik 3 3 3 4 4 . Die Ausgangskachel ist ein Fünfeck ABCDE in
Form eines Rechtecks der Breite a und der Höhe b mit angesetztem gleichschenkligem Dreieck der
Höhe c. Die Signatur ist -15342. Die Nachbar-Bewegung B1 ist also die Achsenspiegelung an EA, B2
die Translation, welche die Seite ED auf die Seite AB abbildet, und B3 bzw. B4 die Punktspiegelung an
der Mitten M3 bzw. M4 von BC bzw. CE. B5 ist die Umkehrabbildung von B2. Der gelbe Punkt P zur
Festlegung einer abgeleiteten archimedischen Kachelung muss so platziert sein, dass sein Abstand von M3
und M4 und von der Seite EA mit der Hälfte der Verschiebungslänge a von B2 übereinstimmt. Darum
muss gelten: . P liegt unter dieser Voraussetzung auf der
Symmetrieachse des Fünfecks im Schnittpunkte der Parabeln mit der Leitgeraden EA und den
Brennpunkten M3 bzw. M4. Diese Parabeln sind die Äquidistanzkurven von B1, B3 bzw. B1, B4.