Es lebe die Geometrie!

Lote gegenüberliegender Kanten beim Viereck
auf der Einheits-Kugel mit nicht komplanaren Eckpunkten

Die Gleitschau zeigt ein Viereck ABCD aus Punkten auf der Fläche der Kugel K vom Radius 1 um
den Koordinaten-Ursprung, die nicht alle vier in einer Ebene liegen. Die sechs Verbindungs-Kanten
sind schwarz mit weißem Mittelstreifen markiert. Zu jedem Paar gegenüberliegender Kanten gibt es
zwei zueinander polare Achsen, die rot, grün oder blau mit grauem Mittelstreifen gezeichnet sind. Um
auszudrücken, dass diese Lote hyperbolisch orthogonal auf den Kanten von ABCD auftreffen, sind
die Lotfußpunkte als Quadrate dargestellt. Jeweils drei der sechs Achsen schneiden sich paarweise
hyperbolisch orthogonal in einem Punkt. Diese vier Achsen-Schnittpunkte bilden darum ein
'Polar-Viereck'. Nur der orangefarbene Punkt Z3 mit schwarzem Zentum liegt im Innern von K, die
anderen drei Punkte Z0, Z1 und Z2 liegen außerhalb von K.

Die Zeichnung zeigt 20 Punkte, nämlich 4 Eckpunkte von ABCD, 4 Eckpunkte des Polar-Vierecks
und 12 Lotfußpunkte. Dieser Punkte verteilen sich so auf die jeweils 6 Kanten-Geraden von ABCD
und dem Polar-Viereck, dass jeweils 4 auf einer dieser Geraden liegen. Die Punkte können dabei so
mit den vier Farben von ABCD gezeichnet werden, dass auf keiner Geraden eine Farbe mehrfach
vorkommt.

In dieser Animation werden zu der Figur der vorangehenden Zeichnung die Geraden zugefügt, die
drei Lotfußpunkte tragen. Anschließend werden die Lotfuß-Verbindungen und die Lotfußpunkte
isoliert dargestellt. Durch jeden dieser 12 Punkte gehen 4 dieser Geraden, und auf jeder dieser
16 Geraden liegen 3 dieser Punkte. Eine derartige Anordnung mit jeweils gleichen Anzahlen von
Geraden durch Punkte und Punkten auf Geraden wird 'Punkt-Geraden-Konfiguration' genannt.
Hier ist es eine -Konfiguration. Dabei ist eine Farbmarkierung möglich, bei der es in
jeder Farbe von ABCD gleich viele Punkte und Geraden gibt. Bei den Geraden durch einen Punkt
kommen diese Farben alle einmal vor. Die Farben der Punkte einer Geraden sind entweder alle
gleich oder es sind drei verschiedene.

In den beiden Teilen dieser Animation wurden nacheinander zu den beiden Seiten-Dreiecken DAB und BCD
des Vierecks ABCD die Fußpunkte der hyperbolischen Lote von den Zentren Z0, Z1, Z2 und Z3 auf die
Dreiecks-Ebene hinzugefügt. Jede Lot-Gerade verbindet ein Zentrum mit dem Pol der Ebene. Diese schneidet
die Einheits-Kugel im Umkreis des Dreiecks. Alle Tangential-Ebenen der Kugel in den Punkten des Umkreises
enthalten den Pol. Er ist in der gleichen Farbe gezeichnet wie der Ebenen-Fußpunkt und dem im Seite-Dreieck
nicht vorkommende Eckpunkt von ABCD. Die Ebenen-Fußpunkte sind in den Farben der zugehörigen Zentren
umrandet. Die Achsen, welche die Zentren Z0, Z1, Z2 und Z3 verbinden, sind hier als dünne Linien in den Farben
magentarot, hellgrün und hellblau dargestellt. Die kleinen weiß gefüllten Kreise geben Punkte auf der Kugel an.

Der Fußpunkt des Lots von zum Beispiel Z3 auf die Ebene eines Seiten-Dreiecks, zum Beispiel DAB, liegt nicht
nur auf der Geraden durch C und dem Pol von DAB, sondern auch auf jeder der drei Geraden, die im Dreieck
hyperbolisch orthogonal zu den Geraden DA, AB bzw. BD sind und DA, AB bzw. BD in ihrem Schnittpunkt P
mit einer Achse treffen. Jede dieser Orthogonalen ist Polare des zweiten Schnittpunkts Q von DA, AB bzw. BD
mit einer Achse bezüglich des Umkreises von DAB. Die Tangenten von Q an den Umkreis berühren diesen also
in Punkten der Orthogonalen. P und Q sind zueinander polar.

Die rot, grün, blau bzw. gelb umrandeten Ebenen-Fußpunkte seien mit F0, F1, F2 bzw. F3 bezeichnet. Je zwei
Ebenen-Fußpunkte Fi und Fj sind mit einem dickeren Strich mit dem Schnittpunkt Fij verbunden, in dem eine
Achse eine Kante von ABCD hyperbolisch orthogonal trifft. Fij ist als farbiges Quadrat mit weißem Kern
gezeichnet. Jede der vier Seiten-Ebenen von ABCD enthält sechs dieser Punkte, wobei je einer auf einer
Verbindungs-Geraden von zwei Ebenen-Fußpunkte liegt. Wenn i, j, k und l vier verschiedene ganze Zahlen
zwischen 0 und 3 sind, dann sind Fij und Fkl Punkte auf einer Kante von ABCD, die bezüglich des Umkreises
des zugehörigen Seiten-Dreiecks zueinander polar sind. Das bedeutet, dass die Verbindungs-Gerade von Fi
und Fj die Polare von Fkl bezüglich des Umkreises ist und die Verbindungs-Gerade hyperbolisch orthogonal
schneidet. Dies ist an den eingezeichneten Tangenten erkennbar.

Die Gleitschau gibt nach den Standbildern der Animation in den letzten zwölf Bildern zusätzliche geometrische
Informationen. In den ersten vier dieser zwölf Bilder sind die räumlichen Polaren der Verbindungs-Geraden
von Zentren und Polen als Linien in den Farben magentarot, hellgrün und hellblau eingezeichnet. Die nächsten
vier Bilder zeigen die Seiten-Ebenen in senkrechter Projektion zusätzlich mit den Polaren von F0, F1, F2 und
F3 bezüglich des Umkreises. Die letzten vier Bilder enthalten hyperbolische Distanzen zwischen F0, F1, F2
und F3 und den Zentren Z0, Z1, Z2 und Z3. Man erkennt zwar zwischen den Zahlen eines dieser Bilder keinen
Zusammenhang. Aber bei allen vier dieser letzten Bildern treten die gleichen Zahlen auf.

Zur Berechnung der Zentren Z0, Z1, Z2 und Z3 und der zugehörigen Lotfußpunkte :

a, b, c und d seien Koordinaten-Tripel der Punkte ABCD. Jeder Punkt Z des affinen Raums kann mit Hilfe
von Koordinaten (r;s;t;u) zur Basis a, b, c, d in der Form dargestellt werden, wobei
die Darstellung eindeutig ist, wenn man die Koordinaten r, s, t, und u so wählt, dass die Summe 1 ergibt. In
diesem Fall nennen wir eine Affin-Kombination von a, b, c und d und (r;s;t;u) ein
Quadrupel von Schwerpunkts-Koordinaten. Wir interessieren uns für die Fußpunkte der Lote von Z auf die
Geraden AB, BC, CD und DA, wobei die hyperbolische Orthogonalität zugrunde gelegt wird. Diese ist durch
die Bilinearform festgelegt. Auf der vorhergehenden Seite wird
erklärt, dass zwei Punkte P und Q genau dann polar zueinander sind, wenn für ihre Koordinaten-Quadrupel
p und q im projektiven Raum gilt: . Zwei Ebenen D und E,
zu denen d bzw. e das Quadupel der Koeffizienten in ihrer Gleichung angibt, sind genau dann orthogonal,
wenn gilt. seien die Quadrupel, die entstehen,
wenn man die Tripel a, b, c und d um eine 1 als vierte Komponente ergänzt. Wir betrachten dann die
Matrix 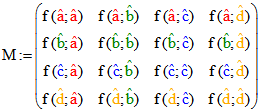, und zu dem Punkt Z mit dem Quadrupel der
Schwerpunkts-Koordinaten (r;s;t;u) das Quadrupel . Dann errechnet man
folgendermaßen die Koordinaten-Quadupel der Fußpunkte der Lote auf die Geraden AB, BC, CD und DA :
, , und .
Man erhält daraus die zugehörigen Koordinaten-Tripel, indem man die ersten drei Komponenten durch die
vierte teilt. Die Lotfußpunkte teilen die Strecken AB, BC, CD und DA im Verhältnis .
Wenn man in den Termen der Fußpunkt-Quadrupel das Plus-Zeichen in ein Minus-Zeichen ändert, ergibt
sich das Quadupel des zum Fußpunkt polaren Punktes auf der Geraden AB, BC, CD bzw. DA , der in den
Animationen ebenfalls eingezeichnet ist.

Anders als für die Punkte Z0, Z1, Z2 und Z3 liegen für einen beliebigen Punkt Z die zugehörigen Fußpunkte
und Z nicht in einer gemeinsamen Ebene. Dennoch sind die Fußpunkte ohne Z komplanar, denn das Produkt
der oben genanten Teilverhältnisse ist 1. Siehe dazu die Seite ' Ceva'. Darum schneiden sich die Verbindungs-
Geraden gegenüberliegender Fußpunkte. Diese Verbindungs-Geraden sind aber im Allgemeinen keine Lot-
Geraden, wohl aber bei den Punkten Z0, Z1, Z2 und Z3.

Zur Erklärung der Terme für Z0, Z1, Z2, Z3 betrachten wir die Determinanten-Gleichung ,
wobei . Dies ist eine lineare Gleichung in den Koordinaten x, y und z, welche die Ebene durch die
Punkte A, B und C beschreibt. Die Vorzahlen von x, y und z und das konstante Glied fassen wir zum Quadrupel
zusammen. Dann ergeben sich folgende Quadrupel für Z0, Z1, Z2 und Z3 :
Z0 :
Z1 :
Z2 :
Z3 :
Unter der hier gemachten Voraussetzung, dass A, B, C, D Punkte der Einheits-Kugelfläche sind,
können die Zahlen unter den Wurzelzeichen auch anders berechnet werden. Es gilt dann nämlich :



Da A und B auf der Einheits-Kugelfläche liegen, ist der euklidischen Abstand
von A und B, denn





.