Es lebe die Geometrie!

Tetraeder, die achsensymmetrisch zu den
gemeinsamen Orthogonalen der Gegen-Kanten sind

->Pdf-Datei https://www.vivat-geo.de/Pdf-Dateien/Tetraeder.pdf

Ein Tetraeder ist achsensymmetrisch zu der gemeinsamen Orthogonalen g eines Paars von Gegen-Kanten,
wenn die Spiegelung an g das Tetraeder auf sich abbildet. Unter der Spiegelung an g verstehen wir dabei
die Drehung um g mit dem Drehwinkel 180° = pi. Wir betrachten auf dieser Seite zunächst den Fall der
euklidischen Geraden-Spiegelung und dann den der hyperbolischen Geraden-Spiegelung. Im ersten Fall
wird der Winkel zwischen zwei Ebenen D und E zu den Gleichungen
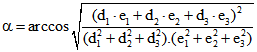und mit der Formel berechnet.
Im zweiten Fall benutzen wir die Abkürzung .
Dann ist , wenn fqn zwischen 0 und 1 (jeweils einschließlich) liegt.
Für fqn >1 ist und für fqn < 0 ist.
Um dazu passend den Abstand von Punkten berechnen zu können, ergänzt man das Koordinaten-Tripel
eines Punktes P des affinen Raums um eine vierte Komponente 1, um ihn in den projektiven
Raum einzubetten. Man kann dann den Abstand zweier Punkte P und Q mit Quadrupeln berechnen,
ähnlich wie bei dem Winkel für Ebenen mit den Quadrupeln und .
(Im euklidischen Fall bleibt die vierte Komponente ungenutzt.)
Siehe dazu auch die Seite ' Höhen im 6-Rechteck'.

Die symmetrische Bilinearform für Ebenen-Quadrupel, die der Maß-Bestimmung zugrunde liegt, ist
für die euklidische Geometrie und für die hyperbolische Geometrie
. Im euklidischen Fall ist f(d;d) stets positiv, kann im 2. Fall
aber auch Null oder negativ sein. Wenn f(d;d) = 0 ist, bedeutet dies, dass die Ebene D die Kugel K
um den Ursprung mit dem Radius 1 berührt.

Wenn ein Tetraeder achsensymmetrisch zu allen drei gemeinsamen Orthogonalen der drei Paare von
Gegen-Kante ist, stimmt im euklidischen Fall die Länge jeder Kante mit der ihrer Gegen-Kante überein.
Die Seiten-Dreiecke des Tetraeders haben dann die gleiche Form und Größe. Wir nennen diese Tetraeder
'gleichseitig' oder 'äquifazial'. Die Form dieser Seiten-Dreiecke ist nur dadurch beschränkt, dass die Größe
aller Innenwinkel zwischen 0 und 90° (jeweils ausschließlich) liegt.

Wenn dagegen im Fall der hyperbolischen Geometrie die Eckpunkte des Tetraeders auf K liegen, kann die
Form und Größe der Seiten-Dreiecke sehr unterschiedlich sein. Dies liegt daran, dass jede Spiegelung,
deren Berechnung auf der Bilinearform basiert, jeden Punkt von
K auf einen Punkt von K abbildet. Darum wird jedes Tetraeder mit Eckpunkten auf K durch Spiegelungen
an gemeinsamen Orthogonalen der Geraden zu Gegen-Kanten auf sich abgebildet. Zu jedem Paar von
Gegen-Kanten gibt es hierbei zwei gemeinsame Orthogonalen, wobei die zugehörigen Spiegelungen
übereinstimmen. Die beiden gemeinsamen Orthogonalen sind zueinander 'polar'.

Im Gegensatz dazu gibt es im Fall der euklidischen Maß-Bestimmung zu jedem Paar von Gegen-Kanten
genau eine gemeinsame Orthogonale, zu der eine Spiegelung existiert. Für gleichseitige Tetraeder ist
charakteristisch, dass diese Spiegelungen das Tetraeder auf sich abbilden, dabei allerdings die Eckpunkte
vertauschen. Die gemeinsamen Orthogonalen der drei Paare von Gegen-Kanten schneiden sich paarweise
senkrecht im Schwerpunkt S, der auch das Umkugel-Zentrum und der Monge-Punkt ist. S ist nur dann
auch Ortho-Zentrum, wenn dieses existiert, und dies ist bei einem gleichseitigen Tetraeder nur dann der
Fall, wenn alle Kanten die gleiche Länge haben.

Unter einem 'Isometrie-Zentrum' eines Tetraeders verstehen wir einen Punkt P, der bei jeder Spiegelung
fest bleibt, die das Tetraeder auf sich abbildet. Dann stimmen also Bild-Punkt und Urbild-Punkt von P
überein. Wir verwenden diesen Begriff nur in den Sonderfällen, in denen es Spiegelungen gibt, die das
Tetraeder auf sich abbilden. Bei euklidischer Maß-Bestimmung hat jedes gleichseitige Tetraeder genau ein
Isometrie-Zentrum, nämlich S. Bei hyperbolischer Maß-Bestimmung gibt es für ein Tetraeder mit Eckpunkten
auf K genau vier Isometrie-Zentren, nämlich die Schnittpunkte der sechs Geraden, an denen es Spiegelungen
gibt, die das Tetraeder auf sich abbilden.

Die Animation zeigt ein gleichseitiges Tetraeder ABCD mit Seiten-Dreiecken, die alle Kanten der Längen
1,45 und 1,50 und 1,10 haben. Die Seiten BCD, CDA und DAB werden um die Kanten BC, CA und AB
gedreht bis sie in der Ebene ABC liegen. Die gedrehten Dreiecke und das Dreieck fügen sich mit ABC zu
dem Dreieck zusammen, das aus ABC durch Streckung mit dem Faktor -2 und dem Schwerpunkt
S von ABC als Zentrum entsteht. Die Seiten dieses Dreiecks sind also parallel zu denen von ABC. Aus der
Vogel-Perspektive zeigt sich, dass der Fußpunkt der Raum-Höhe des Tetraeders durch D der Schnittpunkt
der Flächen-Höhen von ist. Dieser Punkt ist das Bild des Ortho-Zentrums von ABC bei Spiegelung
am Umkreis-Zentrum von ABC. Der weiß gefüllte Punkt dazwischen ist S.

Im gleichseitigen Tetraeder ABCD sind hier die gemeinsamen euklidischen Orthogonalen der
Gegen-Kanten eingezeichnet.Sie treffen diese Kanten in ihrem Mittelpunkt und stehen im Isometrie-
Zentrum S paarweise euklidisch senkrecht zueinander. Die 180°-Drehung um die blaue Orthogonale
bildet ABCD auf BADC ab, die rote auf DCBA und die grüne auf CDAB. Es werden also die
Eckpunkte permutiert. Die Hintereinanderschaltung dieser drei Spiegelungen bildet ABCD auf ABCD
ab, ist also die Identität, die alle Punkte auf sich abbildet. Mit einer dieser Spiegelungen oder der
Hintereinanderschaltung von zweien kann man jeden Eckpunkt in einen beliebigen anderen abbilden
und jedes Seiten-Dreieck in jedes beliebige andere.

Dadurch, dass die Spiegelungen an den drei gemeinsamen euklidischen Orthogonalen der Gegenkanten
ABCD auf sich abbilden, fallen viele geometrisch ausgezeichneten Punkte des Tetraeders zusammen. Denn
zum Beispiel der Monge-Punkt von ABCD wird bei jeder dieser Spiegelungen in den Monge-Punkt des
Bild-Tetraeders, also ABCD selbst abgebildet. Darum bleibt der Monge-Punkt bei allen drei Spiegelungen
fest, muss also der Schnittpunkt S der drei Orthogonalen sein. Aus dem gleichen Grund ist S auch der
Schwerpunkt und das Umkugel-Zentrum von ABCD. Dennoch ist die Geometrie des gleichseitigen
Tetraeders nicht so trivial wie die Geometrie des gleichseitigen Dreiecks. Wenn die Seiten-Dreiecke des
Tetraeders nicht gleichseitig sind, haben die Raum-Höhen keinen gemeinsamen Punkt. Dies gilt auch für
die Verbindung der Eckpunkte mit den Symmedian-Punkten oder Inkreis-Mittelpunkten der Gegen-Seiten.

Dass beim gleichseitigen Tetraeder trotz einiger Vereinfachungen dennoch interessante geometrische Aspekte
auftreten, soll mit der folgenden Animation an Hand der Raum-Höhen gezeigt werden.

Wie auf den Seiten ' Höhen 1' und ' Höhen 2' dargestellt wurde, sind die Raum-Höhen eines nicht
orthozentrischen Tetraeders Geraden eines Regulusses von einem Hyperboloids Q, zu dessen zweiten
Regulus die Orthogonalen der Seiten-Dreiecke von ABCD durch deren Ortho-Zentrum gehören, die
wir 'Ko-Höhen' nennen. Die Ebenen durch das Isometrie-Zentrum S eines gleichseitigen Tetaeders
ABCD, die je zwei der drei gemeinsamen Orthogonalen der Gegenkanten enthalten, sind Symmetrie-
Ebenen von Q. Sie schneiden aus Q eine Ellipse und zwei Hyperbeln heraus. Das erste Bild
der Animation macht nur die Ellipse erkennbar, da der Augenpunkt der Projektion so gewählt wurde,
dass seine Verbindung mit S euklidisch orthogonal zur Ebene der Ellipse ist. Erst nach Veränderung
der Position des Augenpunktes in den folgenden Bildern werden die Hyperbeln erkennbar. Das
zweite und dritte Standbild in der Gleitschau im Anschluss an die Animation zeigen die Orthogonal-
Projektionen zu den anderen beiden Symmetrie-Ebenen mit jeweils einer erkennbaren Hyperbel.

Die drei Zahlen im ersten Bild oben in der Mitte geben die Quadrate der Achsen-Abschnitte der drei
Kegelschnitte an, für die Ellipse die zwei Zahlen ohne Minus-Zeichen und für die Hyperbeln je eine
dieser positiven Zahlen zusammen mit der Zahl mit Minus-Zeichen. Wenn man in den Symmetrie-Ebenen
kartesische Koordinaten-Systeme mit je zwei der drei gemeinsamen Orthogonalen der Gegenkanten von
ABCD einführt, ergeben sich also folgende Gleichungen für die Kegelschnitte:
, und .

In der Animation wird nach der ersten Veränderung des Augenpunktes ein schwarz-graues Viereck
eingezeichnet. Die schwarzen Strecken gehören zu Geraden des Höhen-Regulussen von Q und die grauen
Strecken zu Geraden des Ko-Höhen-Regulusses. Die Eckpunkte liegen abwechselnd auf den beiden
Hyperbeln. Bemerkenswert ist hierbei, dass sich stets vier Regulus-Geraden zu so einem Viereck
zusammenschließen, egal mit welcher Regulus-Geraden man anfängt. Die Spiegelungen an den Symmetrie-
Ebenen bilden jedes dieser Vierecke auf sich ab. Im letzten Teil der Animation werden weitere Regulus-
Geraden gezeichnet. Eine Kachelung des zugehörigen Hyperboloids Q wird in einigen Standbildern nach
der Animation gezeigt.

Wenn man dem gleichseitigen Tetraeder ABCD außen an den Seiten deren Kubus-Spitzen zufügt,
entsteht ein Quader, dessen Zentrum das Isometrie-Zentrum des Tetraeders ist. Daraus folgt,
dass jede der Kubus-Spitzen durch Spiegelung eines Eckpunktes von ABCD am Isometrie-Zentrum
entsteht.

Zur Berechnung eines gleichseitigen Tetraeders :

Die Berechnung eines gleichseitigen Tetraeders vereinfacht sich durch die Gleichungen a = as, b = bs
und c = cs. Teilweise ist auch die Ersetzung
nützlich, wobei gilt. Dies sind die
Abstände der Eckpunkte eines Seiten-Dreiecks von den zugehörigen Kubus-Spitzen (siehe die Seite
' Höhen 2').

Dann ist das Volumen des Tetraeders , der Flächeninhalt der Seiten-Dreiecke
und
jede der vier Höhenlängen 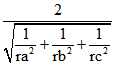. Die Matrix der baryzentrischen Quadrupel der
Höhen-Fußpunkte ist .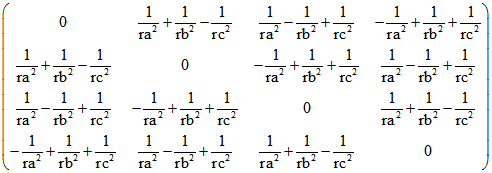

Die Maß-Matrizen G und H, die auf der Seite ' Monge' definiert wurden, vereinfachen sich zu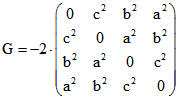

und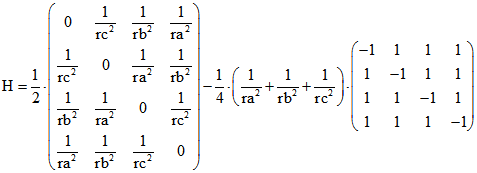


Die Zeilen von H sind die baryzentrischen Quadrupel der Pole von den Seiten-Ebenen des Tetraeders.
Die Verbindungs-Geraden dieser Pole mit einem Punkt P schneiden diese Ebenen also euklidisch
orthogonal in den zu P gehörigen Lotfuß-Punkten. Wenn P das Isometrie-Zentrum S ist, sind diese
Lotfuß-Punkte die Berühr-Punkte der Inkugel. Die i-te Zeile von H ist ein u-Vektor, dessen Länge
den Kehrwert der i-ten Raum-Höhe angibt. u-Vektoren sind Quadrupel mit Komponenten-Summe 0.


Das Quadrat des Abstands zweier Punkte P und Q mit den normierten baryzentrischen Quadrupeln
p und q ist . Für vier Punkte P, Q, R und S ist das euklidische
Skalarprodukt der Verbindungs-Vektoren QP und SR. Wenn QP und SR also orthogonal sind, ergibt
sich also Null. Das ist zum Beispiel der Fall für die Verbindungs-Vektoren (1;1;-1;-1) und (1;-1;1:-1)
der Mitten gegenüberliegender Kanten.

Der Kosinus des Winkels zwischen zwei Ebenen D und E mit den baryzentrischen Quadrupeln
d und e ist gleich .

Damit berechnet man das Quadrat des Radius der Umkugel zu und
den Kehrwert des Quadrats vom Radius der In-Kugel, die alle vier Seiten-Dreiecke von innen berührt, zu
.
Die Ex-Kugeln, die eine der Seiten-Dreiecke von außen berühren, die andern aber auch von der gleichen
Seite wie die In-Kugel, haben Mittelpunkte mit unnormierten Quadrupeln, bei denen das Quadrupel (1;1;1;1)
von S bei einer Komponente durch -1 ersetzt ist. Der Kehrwert des Quadrats ihres Radius ist 1/4 von dem
der In-Kugel. Dieser Kehrwert tritt auch im Kosinus des Winkels zwischen den Seiten-Ebenen auf. Für die
Gegen-Seiten von A und B, sowie C und D ist dies .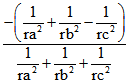

Die Zeilen der Matrix 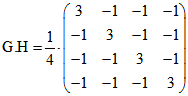sind die baryzentrischen Verbindungs-Vektoren des
Umkugel-Zentrums O mit den Eck-Punkten. Es ist bemerkenswert, dass die Summe dieser Vektoren der
Null-Vektor ist. Dies hat zur Folge, dass O mit dem Fermat-Punkt übereinstimmt. Dieser Punkt ist dadurch
ausgezeichnet, dass die Summe seiner Entfernungen von den Eckpunkten minimal ist. Die Komponente in der
i-ten Zeile und j-ten Spalte von 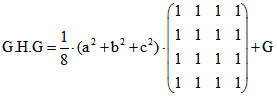gibt das euklidische Skalarprodukt
vom i-ten und j-ten Verbindungs-Vektor an. Wenn man durch das Diagonal-Element teilt,
erhält man den Kosinus des Winkels dazwischen, für i = 1 und j = 2 zum Beispiel .


Mit den Abkürzungen ,
und ergibt sich die Matrix Fp, die auf der Seite ' Höhen 1' zur
Beschreibung des Höhen-Hyperboloids H benutzt wurde, in der Form: .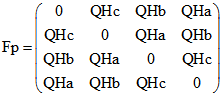
Ein Punkt P mit dem baryzentrischen Quadrupel p liegt genau dann auf der Quadrik H, wenn .
Für das Quadrat der großen Halbachse der magentfarbenen Ellipse errechnet man damit
.

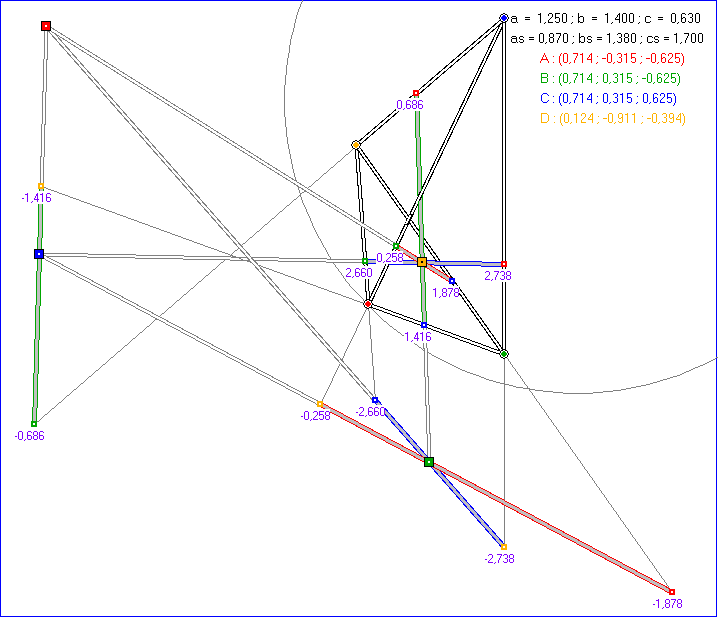
Diese Animation wiederholt Bilder der Seite ' Kugelviereck 1' , auf denen ein Viereck ABCD mit
Eckpunkten auf der Kugel K um den Ursprung mit dem Radius 1 im Rahmen der hyperbolischen
Geometrie dargestellt wird. Als Tetraeder betrachtet hat ABCD die oben rechts im Bild angegebenen
Kantenlängen. Das erste Bild der Animation zeigt zu jedem Paar von Gegen-Kanten zwei gemeinsame
hyperbolische Orthogonalen, deren Schnittpunkte mit den Kanten-Geraden von ABCD durch kleine
Quadrate markiert sind, um die Orthogonalität auszudrücken. Zu jedem Paar von Gegen-Kanten
werden die Strecken der beiden Orthogonalen zwischen ihren Lot-Fußpunkten in der gleichen Farbe
rot, grün oder blau angezeigt. Durch jeden der 12 Lot-Fußpunkte gehen 4 Geraden in den Farben rot,
grün, blau und gelb, und auf jeder der 16 Geraden liegen 3 Punkte. Es ergibt sich so eine
-Punkt-Geraden-Konfiguration. Jeweils drei der sechs Orthogonalen treffen sich hyperbolisch
orthogonal in einem der Isometrie-Zentren Z0, Z1, Z2 oder Z3 , die als große Quadrate dargestellt
werden. Die Existenz hyperbolischer Isometrie-Zentren bei beliebiger Form des Tetraeders ist möglich,
weil hyperbolische Spiegelungen die euklidische Form im Allgemeinen nicht erhalten.

Die baryzentrischen Koordinaten dieser Isometrie-Zentren bezüglich ABCD sind oben links im Bild
angegeben. Der große Buchstabe N bezeichnet dabei die Funktion, die dem unnormierten Quadrupel
eines Raum-Punktes P das normierte Quadrupel von P zuordnet, bei dem alle Komponenten durch die
Summe der vier Komponenten geteilt wird. In der unnormierten Version ist der Betrag jeder Komponente
das Produkt der Kanten-Längen der Seiten-Dreiecke DCB, CDA, BAD und ABC des Tetraeders. Die
Vorzeichen sind dabei für Z0 + - + - , fürZ1 - - + + , für Z2 + - - + und für Z3 + + + + . Aus dem
Quadrupel Z3 ergeben sich Z0, Z1 und Z2 also durch Änderung der Vorzeichen bei zwei Komponenten.
Falls man das Tetraeders mit Eckpunkte auf der Einheits-Kugel K durch ein anderes Tetraeder ersetzt,
ändert sich die Form dieser baryzentrischen Koordinaten für die Isometrie-Zentren nicht. Man muss
dann allerdings für die hyperbolische Maß-Bestimmung statt der Bilinearform
eine entsprechende Bilinearform benutzen, bei der die Nullstellen
der zugehörigen Quadratform nicht zu den Tangential-Ebenen von K gehören, sondern den Tangential-
Ebenen der Umkugel des geänderten Tetraeders.

Nach der Drehung des ersten Bild der Animation werden in einem zweiten Standbild Verbindungs-Geraden
der mit kleinen Quadraten markierten Lot-Fußpunkte zugefügt und im dritten Standbild isoliert angezeigt.
Jeweils drei der Lot-Fußpunkte mit gleicher Farbe oder mit drei verschiedenen Farben liegen auf einer
Geraden.

Die Lot-Fußpunkte zeigen einen bemerkenswerten Zusammenhang zwischen dem Tetraeder ABCD und
dem Tetraeder Z0Z1Z2Z3: Jede Kanten-Gerade durch zwei Eckpunkte P und Q von ABCD oder
Z0Z1Z2Z3 trägt zwei der Lot-Fußpunkte L1 und L2, und diese teilen die Strecke PQ harmonisch.
Das bedeutet, dass der Quotient aus den Abständen von L1 zu P und zu Q mit dem Quotienten aus
den Abständen von L2 zu P und zu Q übereinstimmen, aber nur einer der beiden Punkte zwischen P
und Q liegt. Die Teilverhältnisse sind also im Betrag gleich, aber im Vorzeichen verschieden.

Dieser Zusammenhang drückt sich in Gleichungen mit den baryzentrischen Quadrupeln , , und
von Z0, Z1, Z2 und Z3 aus, zum Beispiel für die Gerade Z1Z2 durch die Gleichungen
und .
Die erste beschreibt das Quadrupel des Lot-Fußpunkts zwischen Z1 und Z2 als Linearkombination der
baryzentrischen Quadrupel (0 ; 1 ; 0 ; 0) von B und (0 ; 0 ; 0 ; 1) von D und zeigt damit, dass der
zugehörige Punkt auf Z1Z2 und BD liegt. Die zweite zeigt Entsprechendes für Z1Z2 und AC. Darin,
dass sich und nur im Vorzeichen unterscheiden, ergibt sich die harmonische
Teilung von Z1Z2.

Sei 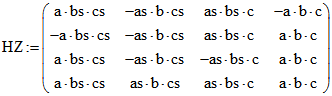. Die Anwendung der Normierungsfunktion N
auf eine Matrix bedeute, dass dadurch N auf jedes Zeilen-Quadrupel angewandt wird. Dann drückt sich
der Zusammenhang zwischen den Tetraedern Z0Z1Z2Z3 und ABCD hinsichtlich der Lot-Fußpunkte
durch folgende Matrix-Gleichungen aus :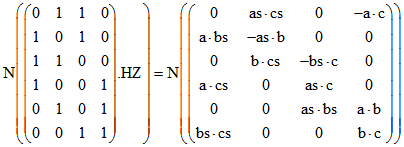
und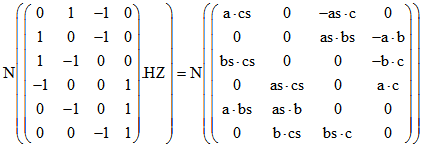



Wenn man in HZ die Zahlen , , , durch das baryzentrische Quadrupel
irgendeines von Z3 verschiedenen Punktes ersetzt, der nicht auf einer Seiten-Ebene von ABCD liegt, und die
Vorzeichen-Kombinationen + - + - , - - + + , + - - + und + + + + beibehält, ergibt sich der gleiche
harmonische Zusammenhang zwischen den Tetraedern Z0Z1Z2Z3 und ABCD .

Die vier Bilder der fogenden Gleitschau zeigen die Teilverhältnisse farbig und die Abstände schwarz an.