Es lebe die Geometrie!

Der Inversor von Peaucellier

Der Inversor von Charles-Nicolas Peaucellier (1832-1919) ist eine Maschine zur Umwandlung
einer Bewegung auf einem Kreis k1 in eine Bewegung auf einem Kreis oder einer Geraden, die
aus k1 durch Spiegelung an einem Kreis k0 oder einer Hintereinanderschaltung dieser Spiegelung
mit der Spiegelung an Zentrum von k0 entsteht, die wir 'Anti-Kreisspiegelung' nennen. Die Maschine
setzt sich aus vier drehbar zu einer Raute verbundenen Stangen zusammen, bei der ein Eckpunkte
auf k1 und zwei der drei übrigen auf einem weiteren Kreis k2 geführt werden. Der vierte Eckpunkt
bleibt dann auf dem Kreis oder der Geraden, die bei Spiegelung oder Anti-Spiegelung von k1 an
einem Kreis mit dem Radius um den Mittelpunkt M2 von k2 entsteht, wobei der
Radius von k2 ist und s die Seitenlänge der Raute. Eine Umwandlung der Kreis-Bewegung in eine
geradlinige Bewegung kommt dann zustande, wenn k1 durch M2 geht.

Die Animation zeigt den Invertor mit den Daten . Dabei ist
der Radius des dunkelroten Kreises k1 mit dem Zentrum M1 und A als Eckpunkt der Raute
auf k1. ist der Radius des hellroten Kreises mit M2 als Mittelpunkt und den Punkten B und
C (weiß gefüllt) auf k2 . d ist der Abstand der Mittelpunkte und s die Länge der Sehne AB.
Der vierte Eckpunkt D der schwarzen Raute bewegt sich auf der violetten Geraden g.

Begründung (siehe dazu das Bild 1 und Bild 2 der Gleitschau):

Sei u der Abstand M2 von A, v der Abstand M2 von D und w der Abstand A vom Mittelpunkt Z der
Raute, der nicht eingezeichnet ist. Außerdem sei e bzw. f der Abstand M2 bzw. C von Z. Dann gilt
. Darum ergibt sich D
aus A durch Spiegelung an dem Kreis um M2 mit dem Radius , der schwarz eingezeichnet ist.

In der zweiten Periode der Animation ist die Enveloppe der Rauten-Diagonalen dunkelblau eingezeichnet,
die hier eine Ko-Sehne darstellt, und hellblau die Pol-Kurve dieser Ko-Sehne. Die Enveloppe ist für die
oben angegebenen Daten eine Parabel und die Pol-Kurve ein Ellipsenbogen, da ist und
. Dies kann analog zum Beweis am Schluss der Seite zu den Zickzacks
in folgender Weise gezeigt werden :

Sei . Die Ko-Sehne k zum Punkt hat damit die Gleichung
. Der Schnittpunkt von k mit der Ursprungsgeraden durch A ist der
Punkt . Er liegt also auf der Parabel mit dem Hallbparameter p,
dem Brennpunkt im Urspung und der kartesischen Gleichung . Die Tangente in H hat
die Gleichung . Die Polare des Poles J der Ko-Sehne hat die Gleichung
. Durch Koeffizienten-Vergleich ergibt sich daraus
und 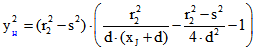. Daraus folgt für die
Pol-Kurve die Kegelschnitt-Gleichung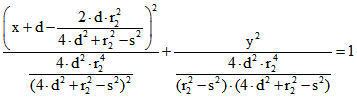

Die Daten dieses Inversors sind . Gegenüber der vorherigen
Animation ist also nur die Sehnenlänge vergrößert worden, so dass sie jetzt größer als ist.
Die durch den Inversor erzeugte Abbildung ist hier keine Kreisspiegelung, sondern eine
Hintereinanderschaltung der Spiegelung an dem schwarzen Kreis und der Spiegelung an
seiner Kreismitte M2, also eine Anti-Kreisspigelung. Der Radius des schwarzen Kreises ist
. Wegen der Lage von M2 auf dem roten Kreis bewegt sich auch hier der vierte
Rautenpunkt D auf einer Geraden, und die blaue Enveloppe der Diagonalen ist eine Parabel.
Die hellblaue Pol-Kurve ist jedoch kein Ellipsen-Bogen, sondern ein Hyperbel-Bogen-Paar.

Daten des Inversors :

Bild 1 und 2 :
Bild 3 :