Es lebe die Geometrie!

Raum-Höhen im Tetraeder 1

-> Pdf.Datei https://vivat-geo.de/Pdf-Dateien/Tetraeder.pdf

Unter einer Raum-Höhe in einem Tetraeder ABCD verstehen wir eine Gerade durch einen der Eckpunkte
A, B, C oder D , die euklidisch orthogonal zur Ebene der gegenüberliegenden Seitenfläche verläuft (z.B.
durch A senkrecht zu BCD). Wir unterscheiden sie von einer Flächen-Höhe, die eine Gerade durch einen
Eckpunkt ist, die euklidisch senkrecht zu einer Kanten-Geraden in der Fläche der Gegen-Seite steht (z.B.
durch A senkrecht zu BC). Drei Flächen-Höhen in der Fläche einer Seite des Tetraeders haben stets einen
gemeinsamen Schnittpunkt (das 'Orthozentrum' der Seite), die vier Raum-Höhen aber nur dann, wenn die
Richtungs-Vektoren gegenüberliegender Gegen-Kanten orthogonal sind. ABCD heißt dann 'orthozentrisch'.

Unter der 'Ko-Höhe' einer Raum-Höhe h des Tetraeders verstehen wir die Parallele zu h durch das
Orthozentrum der zu h orthogonalen Tetraeder-Seite. hat mit jeder der von h verschiedenen Raum-
Höhen einen gemeinsamen Punkt (x;y;z) des affinen Raums. Mit h selbst gibt es nur im orthozentrischen
Tetraeder gemeinsame Punkte des affinen Raums, weil dann h und zusammenfallen. Andernfalls
haben diese beiden Geraden nur den 'unendlich fernen' Punkt in der projektiven Erweiterung des affinen
Raums gemeinsam, der auf allen Parallelen zu h liegt. Dieser wird durch ein kartesisches Quadrupel (x;y;z;0)
beschrieben, wobei (x;y;z) einen Richtungs-Vektor von h angibt.

Schon drei der vier Raum-Höhen von ABCD bestimmen eindeutig das Hyperboloid H, das aus den Punkte
der Geraden besteht, die alle drei Raum-Höhen schneiden. Wählt man drei andere Raum-Höhen aus, so
ergibt sich die gleiche Punktmenge, auch dann, wenn man statt der Raum-Höhen ihre Ko-Höhen nimmt.
Keine der Geraden, die drei Raum-Höhen h, j und k schneiden, stimmt mit einer Geraden überein, welche
die drei Ko-Höhen , und schneidet, und keine der Geraden, die , und schneiden,
stimmt mit einer Geraden überein, welche h, j und k schneiden. Jede dieser beiden disjunkten Geraden-
Mengen bezeichnet man als Regulus. Die zweite nennen wir Höhen-Regulus, weil sie alle Raum-Höhen
enthält und die erste Ko-Höhen-Regulus, weil darin alle Ko-Höhen liegen. Jeder Punkt P des Hyperboloids
liegt auf genau einer Geraden des Höhen-Regulusses und einer des Ko-Höhen-Regulusses. Die Ebene durch
diese beiden Geraden nennen wir 'Tangenten-Ebene' des Hyperboloids in P. In jeder anderen Ebene liegt
höchstens eine Gerade der Vereinigungsmenge der beiden Regulusse. Zwei Geraden des gleichen Regulusses
haben also nie einen gemeinsamen Punkt und liegen nie gemeinsam in einer Ebene.

Das erste Bild dieser Animation zeigt die Raum-Höhe des Tetreders ABCD durch den Punkt D und die
zugehörige Ko-Höhe durch das Orthozentrum der Seite ABC. Die beiden Geraden liegen spiegelbildlich
zum eingezeichneten Monge-Punkt. Für die Daten des Tetraeders wurden die gleichen Bezeichnungen wie
auf der vorhergehenden Seite ' Monge' benutzt.

Im zweiten Bild wird eine Kubus-Spitze K der Seite ABC zugefügt, von der aus die Kanten AB, BC und
CA unter einem Sehwinkel von 90° erscheinen. Es gibt nur einen weiteren Punkt mit dieser Eigenschaft. Er
entsteht durch Spiegelung von K an der Ebene ABC. Die Ko-Höhe verbindet beide Punkte. In der letzten
Animation der folgenden Seite ' Höhen 2' wird die besondere Bedeutung der Kubus-Spitzen bei einem
orthozentrischen Tetraeder erkennbar. Zu einem räumlichen Dreieck gibt es die beiden Kubus-Spitzen
genau dann, wenn die Größe von allen drei Innenwinkeln des Dreiecks kleiner als 90° ist.

Das dritten Bild zeigt auch das Tetraeder, das durch Spiegelung von ABCD am Monge-Punkt entsteht, für
das die Rollen von Raum-Höhe und Ko-Höhe vertauscht sind. Das vierte bis siebente Bild zeigt das Paar aus
Raum-Höhe und-Ko-Höhe für die Eck-Punkte C, A und B.

Das achte Bild zeigt alle Raum-Höhen und Ko-Höhen mit ihren Schnittpunkten. Die doppelt gekreisten
Punkte auf den Raum-Höhen sind die Schnittpunkte mit den Seiten-Ebenen, auf denen sie senkrecht stehen.
Der Höhen-Abschnitt bis zum zugehörigen Eck-Punkt ist dicker gezeichnet. Im neunten Bild sind die
Schnittpunkte K, L, M, N der Raum-Höhen zu A und C mit den Ko-Höhen zu B und D durch ein farbiges
Viereck hervorgehoben. Das zehnte Bild zeigt zusätzlich ein entsprechendes Viereck mit vertauschten Rollen
von Raum-Höhen und Ko-Höhen.

Im elften Stand-Bild der Animation ist in das Viereck KLMN die magentafarbene Ellipse mit dem Monge-
Punkt als Zentrum eingefügt, die sich beim Schnitt des zu den Regulussen gehörigen Hyperboloids H mit einer
seiner Symmetrie-Ebenen ergibt. Jede Kante von KLMN hat einen Punkt mit der Ellipse gemeinsam, keine
der Kanten liegt aber in ihrer Ebene. Auf einen algebraischer Weg zur Berechnung dieser Ebene wird unten
auf dieser Seite hingewiesen. Leider fehlt eine geometrische Konstruktion für diese Ebene.

Die Konstruktion des elften Bild wird um 130° gdreht, um die räumliche Anordnung zu verdeutlichen. Dann
wird ein Schar blauer Ellipsen gezeigt, die sich ergibt, wenn man das Hyperbolid H mit Ebenen parallel zu
der von E schneidet, zusammen mit den Schnittpunkten von Raum-Höhen und Ko-Höhen. Die weitere
Drehung macht die Form von H erkennbar.

Ausgehend von dem Basis-Viereck KLMN mit der magentafarbenen Ellipse der vorhergehenden Animation
wird hier eine Schar von Regulus-Geraden des Hyperboloids H aufgebaut. Das Verfahren entspricht dem auf
der Seite ' Ceva', wobei das Viereck KLMN die Rolle des dort mit ABCD bezeichneten Vierecks übernimmt.
Die Anpassungen der Berechnungen im Viereck KLMN werden auf der folgenden Seite ' Höhen 2' dargestellt.
Die schwarzen Geraden schneiden alle vier Raum-Höhen, gehören also zum Ko-Höhen-Regulus. Die grauen
Geraden im Ko-Höhen-Regulus treffen alle vier Raum-Höhen. Jede Regulus-Gerade schneidet die Ellipsen-
Ebene, also auch die Ellipse selbst. Die beiden dick gezeichneten schwarzen Geraden g und g' des Ko-Höhen-
Regulusses treffen sie in zum Monge-Punkt spiegelbildlichen Punkten. Durch diese Punkte gehen auch die dick
gezeichneten grauen Geraden j und j' des Höhen-Regulusses. g ist parallel zu j' und g' parallel zu j. Diese vier
Geraden werden zweimal um die Ellipse herumgeführt. Beim ersten Umlauf legt g in regelmäßigen Abständen
eine schwarze Gerade ab, beim zweiten Durchlauf auch g', so dass zusätzlich eine Reihe von Schnittpunkten
entsteht. Zwischen den beiden Umläufen wird das Hyperboloid gedreht und danach wieder zurückgedreht.

Die Animation zeigt den Aufbau des Hyperboloids mit Hilfe von Kacheln.


Zur Gleichung eines Hyperboloids H, zu dem drei paarweise nicht komplanare Geraden g, h und j
Regulus-Geraden sind :

Die Geraden g, h und j seien durch die Tripel-Paare ; (u;v) und (w;x) in
Plücker-Koordinaten gegeben.
(--> https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf (**)).
Dies können kartesische Plücker-Koordinaten sein oder auch die schon am Schluss der vorherigen
Seite ' Monge' genannten baryzentrischen Plücker-Koordinaten. Im zweiten Fall muss auch für Punkte
und Ebenen in baryzentrischen Koordinaten gerechnet werde. Sei P mit dem Quadrupel p ein Punkt,
der nicht auf g liegt und für den die Ebene E durch P und g nicht h enthält.. Mit der Plücker-Matrix
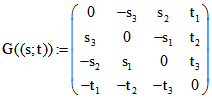ergibt dann p.G((s;t)) ein Quadrupel von E. Mit der zu G((u;v)) dualen
Matrix ist dann q := p.G((s;t)).G((v;u)) Quadrupel eines Schnittpunkts Q von E
und h. Die Gerade PQ mit dem Tripel-Paar

schneidet dann beide Geraden g und h. Dieses Tripel-Paar wird in dem oben genannten Text (**) mit
bezeichnet. Die Gerade PQ schneidet auch die Gerade j genau dann, wenn die Zahl
gleich Null ist.
Genau dann ist PQ eine Gerade des zweiten Regulusses des Hyperboloids H, zu dem g, h, j im ersten
Regulus liegen. P ist darum genau dann Punkt von H, wenn
ist.
Dies ist ein Term, der quadratisch in den Komponenten von p ist und linear in denen von s, t, u, v, w und x.
Man kann diese Gleichung in Matrix-Schreibweise mit einer 4*4-Matrix Fp durch = 0 beschreiben,
wobei die als Spalte geschriebene, also transponierte Form der Zeile p ist.

Um die Matrix Fp übersichtlich darzustellen, benutzen wir die Matrizen
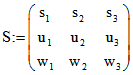und .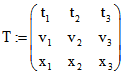
Die Adjunkte von S ist die Matrix 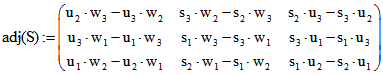, in deren
Spalten man Kreuz-Produkte erkennt und die für ein invertierbares S mit übereinstimmt.
Wir definieren und , außerdem
,, und .
Dabei ist die Matrix, die dadurch entsteht, dass man ST an der Haupt-Diagonalen spiegelt, so dass
STp und TSp durch Spiegelung an der Haupt-Diagonalen unverändert bleiben und STm und TSm in -STm
und -TSm übergehen.
Dann ist .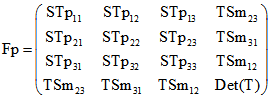
Wenn hier T durch S ersetzt und S durch T, entsteht die Matrix F mit der Eigenschaft, dass die Ebene E mit
dem Quadrupel e genau dann Tangenten-Ebene von H ist, wenn gilt. Das Matrix-Produkt Fp.F
enthält außerhalb der Haupt-Diagonalen nur Nullen und in der Haupt-Diagonalen lauter gleiche Zahlen.

Eine Gerade g mit der Plücker-Matrix G((s;t)) ist genau dann Regulus-Gerade des Hyperboloids zu F,
wenn die Matrix aus lauter Nullen ist. Denn wenn g Regulus-Gerade ist und P ein
Punkt, der nicht auf g liegt, dann ist die Ebene E durch g und P Tangenten-Ebene mit dem Quadrupel
e := p.G((s;t)) und folglich für alle nicht auf g liegende Punkte P.
Und diese Argumentation lässt sich umkehren..

Zur Berechnung der Symmetrie-Ebene E durch den Monge-Punkt, in der die magentafarbene Ellipse der
vorangehenden Animationen liegt, geht man von den kartesischen Plücker-Koordinaten dreier Geraden des
gleichen Regulusses des Hyperboloids aus, zum Beispiel von den Höhengeraden g, h und j durch die Punkte
A, B und C . Die drei Eigenvektoren der Matrix STp sind euklidisch orthogonal zu den drei Symmetrie-
Ebenen des Hyperboloids. Diese errechnet man mit Hilfe der Lösungen x der 'charakteristischen' Gleichung
, also mit Hilfe der 'Eigenwerte' von STp. Ein zum Eigenwert x gehöriger Eigenvektor v
ist dann eine Lösung der Gleichung .

Die baryzentrischen Plücker-Koordinaten von j, h und j ergeben sich, indem man für das Punkt -Quadrupel
p im Term die baryzentrischen Punkt-Koordinaten von A bzw. B bzw. C einsetzt und für q
die erste bzw. zweite bzw. dritte Zeile der am Schluss der vorangehenden Seite 'Monge' genannten Matrix H.
Diese Zeilen geben die unendlich fernen Punkte der Höhen durch A, B und C an. Für die Höhe durch A ist also
p = (1;0;0;0) und q proportional zu



,
wobei die erste Komponente nach der Formel von Heron aus dem 1. Jahrhundert das Quadrat des vierfachen
Flächen-Inhalts vom Dreieck BCD mit Minus-Zeichen angibt. Dann ist (1;1;1;1).F (nicht normiertes)
baryzentrisches Quadrupel des Monge-Punktes.

Plücker-Koordinaten einer Geraden g lassen sich nicht nur mit Hilfe zweier verschiedener Punkte P und Q auf
g berechnen, sondern auch mit Hilfe zweier verschiedener Ebenen D und E, die sich in g schneiden. Wenn d
und e die zugehörigen Quadrupel sind, dann ist

Tripel-Paar von g in Plücker-Koordinaten. Hier sind im Vergleich zur Berechnung mit Punkten Kreuz und
Doppel-Kreuz vertauscht. Diese Berechnung ist sowohl für kartesiche als auch für baryzentrische Koordinaten
anwendbar. Wenn die Matrix ist, deren Zeilen die um eine 1 ergänzten kartesichen Koordinaten-Tripel
von A, B, C und D sind und die Matrix, die durch Spiegelung an der Haupt-Diagonalen entsteht, ergibt
das zu D gehörige baryzentrische Quadrupel. Das baryzentrische Tripel-Paar von g ist dann
.
Eine entsprechende Formel gibt es auch dann, wenn man von zwei Punkt-Quadrupeln p und q ausgeht. Es gilt
.
Wenn man die Plücker-Matrix G((s;t)) von g erst mit Hilfe von e und d und dann mit p und q berechnet ergibt
sich kein Wiederspruch, denn