Es lebe die Geometrie!

Spiegelungen auf der Kugel

--> Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum I
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf

Der gelb umrandete schwarze Punkt P bewegt sich auf der z-Achse des kartesischen Koordinaten-
Systems, in dessen Ursprung der Mittelpunkt der Kugel mit dem Radius 1 liegt. Falls der Punkt P
nicht auf der Kugelfläche liegt, bestimmt er eine eineindeutige Abbildung der Punktmenge der
Kugelfläche, die einem Punkt Q den zweiten Schnittpunkt der Fläche mit der Verbindungsgeraden
von P mit Q zuordnet. Wir bezeichnen als Spiegelung an P.

Wenn P innerhalb der Kugel liegt, hat keine Fixpunkte. Für ein P außerhalb der Kugel bleiben
genau die Punkte fest, die auf der zu P polaren Ebene liegen. Es sind dies die Berührpunkte der
Tangenten von P an die Kugel. Sie liegen auf dem Kugel-Kreis , der in der Animation schwarz
markiert ist. Er ist orthogonal zu jedem Kugel-Kreis, der einen Punkt Q mit seinem Spiegelbild
verbindet. Wir bezeichnen für ein P außerhalb der Kugel auch als Spiegelung an .

Man kann in folgender Weise zu einer Spiegelung des ganzen dreidimensionalen Raums fortsetzen:
Sei Q ein beliebiger Punkt des Raums. Dann gibt es drei Ebenen, die nur den Punkt Q gemeinsam haben
und die Kugel in drei Kreisen schneiden. Die Spiegelbilder bei von diesen Kreisen liegen in Ebenen,
die ebenfalls nur einen gemeinsamen Punkt haben. Dieser Punkt Q' ist unabhängig von der Wahl der
Ebenen durch Q. Er sei das Spiegelbild von Q. Mit dieser Definition wird eine Abbildung, die
kollineare Punkte A, B und C in kollineare Punkte A', B' und C' abbildet und komplanare Punkte
A, B, C und D in komplanare Punkte A', B', C' und D'.

In dieser Animation wird der magentafarbene Kreis K0 an dem blauen Kreis K1 in den roten
Kreis K2 gespiegelt. Der Beträge der euklidischen Winkelgrößen zwischen K0 und K1 sowie
K1 und K2 stimmen überein. Die magentafarbene Gerade g verbindet die gemeinsamen Punkte
von K0, K1 und K2. Auf der zu g polaren Geraden h liegen die Pole dieser drei Kreise. h und
der grüne Kreis K3 liegen gemeinsam in einer Ebene. K3 ist orthogonal zu allen Kreisen der
Kugelfläche durch die beiden Schnittpunkte von g mit der Kugelfläche. Die Spiegelung an K1
bildet die Punktmenge von K3 auf sich ab. Darum geht eine Gerade durch den Pol von K1,
die einen Schnittpunkt von K0 und K3 trifft, auch durch einen Schnittpunkt von K1 und K3.
Zeitweise ist in der Animation auch eine hellblauer Kreis K4 zu sehen, der orthogonal zu K1 ist.
Die Spiegelung an K4 bildet ebenfalls K0 in K2 ab.

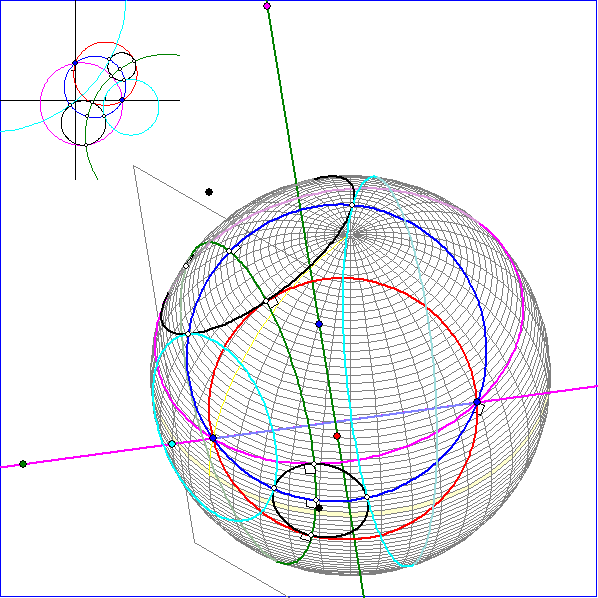
Die schwarzen Kreise berühren die Kreise K0 und K2 in den Schnittpunkten dieser Kreise mit
dem grünen Kreis K3. Die gemeinsamen Tangenten gehen darum durch den Pol P3 von K3. Die
Spiegelungen an den zueinander orthogonalen blauen Kreisen K1 und K4 bilden K0 in K2 ab und
K3 auf K3. (K4 ist nicht in jedem Bild sichtbar.) Darum werden bei diesen Spiegelungen die
Punktmengen von jeweils zwei der schwarzen Berührkreise festgelassen oder vertauscht. Die
hellgrünen und die hellblauen Kreise berühren die schwarzen Kreise in ihren Schnittpunkten mit K1
bzw. K4 und sind hierzu orthogonal. Ihre Ebenen schneiden sich in der grünen Geraden, die auch in
der Ebene von K2 liegt.

Aufeinanderfolgende Bilder geben eine Ansicht der gleichen Kreise aus unterschiedlichen Blickwinkeln.

Zur Rechnung mit Koordinaten :

Für eine übersichtliche Darstellung der Formel zur Berechnung der zur Einheitskugel
gehörigen Spiegelungen ist es sinnvoll, den affinen Raum mit Koordinaten (x ; y; z) zu einem projektiven
Raum mit Koordinaten (x ; y ; z ; u) zu erweitern . Für u = 1 beschreibt dieses Quadrupel den gleichen
Punkt wie das Tripel (x ; y ; z). Für u = 0 werden auch die Punkte der 'unendlich fernen' Ebene erfasst,
um die man sich den affinen Raum erweitert denken kann. Das Quadrupel (x ; y; z ; 0) beschreibt darin
den unendlich fernen Punkt, der auf allen Geraden des affinen Raums liegt, die den Richtungsvektor
(x ; y ; z) haben, also parallel zu der Geraden durch die beiden affinen Punkte (0 ; 0 ; 0) und (x ; y ; z)
sind. Es werden auch Quadrupel mit Werten für u ungleich 1 und 0 benutzt. Diese beschreiben aber
keine zusätzlichen Punkte, da Quadrupel identifiziert werden, deren vier Komponenten sich um den
gleichen Faktor unterscheiden. Das Quadrupel (6 ; 4 ; 8; 2) beschreibt also den gleichen Punkt, wie
das Quadrupel (3 ; 2 ; 4 ; 1), nämlich den affinen Punkt mit x = 3, y = 2 und z = 4. Diese Identifikation
vereinfacht die Rechenterme erheblich. Das Quadrupel (0 ; 0 ; 0 ; 0) beschreibt keinen Punkt.

Zur Bezeichnung eines Koordinaten-Quadrupels für einen Punkt P oder X benutzen wir im Folgenden statt
der Angabe in der Form (x ; y ; z ; u) die Bezeichnung bzw. ,
um den Zusammenhang mit P bzw. X deutlicher zu machen.

Wenn und Quadrupel zu den projektiven Punkten P und Q sind, gehört die Menge der Quadrupel
mit reellen Zahlen r und s zu der Geraden
durch P und Q, falls P und Q nicht zusammenfallen. Wenn statt zweier verschiedener Punkte P und Q drei
Punkte gegeben sind, die nicht gemeinsam auf einer Geraden liegen, beschreibt die Menge der analogen
Linearkombinationen dreier Quadrupel die Ebene durch diese drei Punkte.

Wenn der Pol P einer Ebene nicht gerade der Mittelpunkt der Einheitskugel ist, wird die Ebene durch die
Gleichung beschrieben, also zum Beispiel für durch
. Wenn P im Mittelpunkt liegt, ist die Polarebene die Menge aller unendlich fernen Punkte und
wird durch die Gleichung angegeben. Man kann diesen Sonderfall mit berücksichtigen, indem man
die Gleichung der Ebene zum Pol P durch beschreibt. Da zwei Kreise
auf der Kugeloberfläche genau dann orthogonal zueinander sind, wenn der Pol der Ebene des einen Kreises
auf der Ebene des anderen Kreises liegt, sind die Kreise genau dann orthogonal, wenn für die Pole P und
Q der Ebenen gilt: . Diese Gleichung ist also die Bedingung dafür, dass
P polar zu Q ist. Die Bezeichnung 'polar' benutzen wir auch dann, wenn P oder Q nicht außerhalb der Kugel
liegt und darum kein Kugekkreis zugeordnet ist. Wenn P innerhalb der Kugel liegt, trifft die zugehörige
Polarebene die Kugel nicht, so dass ein zu P polarer Punkt Q außerhalb der Kugel liegen muss.

Jedem Paar von Quadrupeln ordnen wir mit einer Funktion f in folgender Weise eine reelle Zahl zu :

(f ist im Wesentlichen die Bilinearform der speziellen Relativitätstheorie.)

f ist folglich so definiert, dass zwei Kugelkreise genau dann orthogonal sind, wenn für die Pole P und Q
der zugehörigen Ebenen gilt : . f ist eine symmetrische Bilinearform, denn bei Vertauschung
der Quadrupel ändert sich der Funktionswert nicht und es gilt .

Wir nennen die Zahl den 'Quadratformwert' von . Es gilt bzw.
bzw. genau dann, wenn zu einem Punkt P auf bzw. innerhalb bzw. außerhalb der
Oberfläche der Einheitskugel gehört. Im Fall bzw. kann man P stets durch
ein Quadrupel beschreiben, dessen Quadratformwert bzw. ist, indem man eventuell alle
Koordinaten durch teilt. Wir nennen dann 'normiert'.

Es sei nun P ein Punkt des Raumes, der nicht auf der Oberfläche der Einheitskugel liegt. X sei irgendein
Punkt des Raums . Dann ist ein Quadrupel vom Spiegelbild-Punkt
und es gilt . Wir benutzen
die Bezeichnung auch für die lineare Abbildung der Quadrupel. Wenn man
durch ersetzt mit einer reellen Zahl c ungleich Null, ändert sich das Ergebnis nicht. Für einen
Punkt X der Polarebene zu P gilt und folglich . Darum ist X Fixpunkt. Aus
folgt dies auch für P selbst. Wegen bildet die Kugeloberfläche,
das Kugel-Innere und das Kugel-Äußere jeweils in sich ab. Aus

folgt , dass diese Abbildung sogar surjektiv ist, also jeder Punkt als Bildpunkt vorkommt.

Im Fall ist


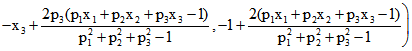
Wenn die vierte Komponente ungleich Null ist und man dadurch teilt, um dort eine 1 zu erzeugen,
erhält für das Tripel der ersten drei Komponenten

.

Um beurteilen zu können, ob es zu zwei Punkten X und Y des Raums eine Spiegelung an einem
Punkt P gibt, die X in Y abbildet, ist folgender Satz nützlich, insbesondere auch für die Seite
' Dreiseite ohne Ecken':

Satz : Für verschiedene Punkte X und Y des projektiven Raums sind diese Eigenschaften äquivalent:
1) X und Y liegen beide auf der Oberfläche der Einheitskugel oder beide nicht; in dem zweiten
Fall werden X und Y aber nicht durch die Oberfläche getrennt.
2) Es gibt einen projektiven Punkt P, so dass X durch die Spiegelung an P in Y abgebildet wird.

Beweis: Aus 1) folgt 2) : Zu X und Y gibt es Quadrupel und , so dass und
beide Null, beide positiv oder beide negativ sind. Im zweiten und dritten Fall seien die Quadrupel
normiert, der Quadratformwert also 1 bzw. -1. Im ersten Fall ist , da es neben
X und Y keine weiteren Punkte der Geraden XY auf der Oberfläche geben kann. Im zweiten und
dritten Fall ist oder , denn

.
Wenn hier ist , ersetzen wir durch , um im Folgenden für einen
Quadratformwert ungleich Null voraussetzen zu können. Dann ist definiert und es
gilt .

Aus 2) folgt 1) : Wenn vorausgesetzt wird und bzw. normierte Quadrupel zu X und Y
sind, dann sind ihre Quadratformwerte nach obiger Rechnung gleich. q.e.d.


Die stereographische Projektion eines Kreises K auf der Kugeloberfläche ergibt einen Kreis K' in
der Tangentialebene des Nordpols, dessen Mittelpunkt und Radius sich in einfacher Weise aus
dem Koordinaten-Quadrupel des Pols P von K ergibt: Es sei nämlich . Dann hat
der Mittelpunkt von K' die Koordinaten und . Der Radius ist .
Der Mittelpunkt ist der Schnittpunkt der Geraden durch den Südpol und P mit der Tangentialebene
im Nordpol.