Es lebe die Geometrie!
Hauptmenü
- Home
- Geometrie 1
- Geometrie 2
- Epizykeltheorie
Addition von Vierecken
Geometrie 2 > Addition von Figuren
Addition von Vierecken mit vorgegebenen Seiten-Richtungswinkeln
Auf dieser Seite werden Polygone mit vier gerichteten Seiten untersucht, bei denen die Richtungswinkel
entsprechender Seiten gleich sind. Die Richtungswinkel mit Werten zwischen 0° und 360° sind dabei in
eine monoton wachsende Reihenfolge gebracht oder ergeben sich aus einer derartigen Reihenfolge durch
zyklische Rotation. Die Seitenlängen werden mit einem Minus-Zeichen versehen, wenn man sich bei einem
Durchlauf des Randes mit zunehmenden Richtungswinkeln gegen die Seiten-Richtung bewegt. Dabei ist die
Seitenlänge Null zulässig.
Die Drehpunktfunktion eines derartigen Vierecks ist eine Treppenfunktion, deren vier Stufen die Längen der
Seiten als Stufen-Differenzen haben und die Richtugswinkel als Sprungstellen. Die Addition der Vierecke
ergibt sich dann aus der bildweisen Addition der Drehpunktfunktionen und die Bestimmung des signierten
Flächeninhalts durch das Stieltjes-Integral ![]() (siehe dazu die Seite
(siehe dazu die Seite
' orthogonale Figuren 1'). Der gemischte Flächeninhalt zweier Polygone wird dann gegeben durch![]() .
.
Die Polygone zu f und g heißen orthogonal, wenn A(f ; g) = 0 ist, also der Flächeninhalt des Polygons zu
f + g die Summe der Flächeninhalte zu f und zu g ist. Für Polygone mit vorgegebenen Seiten-Richtungswinkeln
kann der gemischte Flächeninhalt in entsprechender Weise auch mit Hilfe einer Matrix berechnet werden. Dazu
wird jedes Polygon durch die Folge der Seitenlängen beschrieben, passend zu der Folge der Richtungswinkel.
Diese Folge wird dann als Vektor in Zeilen- oder Spalten-Form angegeben. Zur Flächeninhalts-Bestimmung
benutzt man bei Richtungswinkeln ![]() die Matrix
die Matrix ![]() mit
mit ![]() für j und k zwischen
für j und k zwischen
1 und der Eckenzahl n. Wenn die Vektoren ![]() und
und ![]() in Zeilenform zwei Polygone beschreiben, dann gilt für
in Zeilenform zwei Polygone beschreiben, dann gilt für
ihren gemischten Flächeninhalt ![]() , wobei
, wobei ![]() den Seiten-Vektor in transponierter Form, also
den Seiten-Vektor in transponierter Form, also
in Spaltenform beschreibt.






Die Animation zeigt Vierecke zu den Richtungswinkeln ![]() .
.
Die beiden oberen Vierecke mit dem roten bzw. grünen Startpfeil sind die beiden Tangentenvierecke zu
diesen Richtungen, die einen Einheitskreis einschließen. Diese sind orthogonal zueinander. Das
Viereck oben links zum Seiten-Vektor ![]() ist hellgrün gefüllt, weil der
ist hellgrün gefüllt, weil der
Flächeninhalt positiv ist, und das Viereck oben rechts zu ![]() magentafarben,
magentafarben,
weil der Inhalt negativ ist. Das Viereck zu g hat die Umfangslänge ![]() Null, während
Null, während
bei dem zu f die alternierende Umfangslänge ![]() Null ist. Der Mittelpunkt des
Null ist. Der Mittelpunkt des
Inkreises zu f hat von allen Seiten den signierten Abstand +1, während der signierte Abstand des
Mittelpunkts vom Inkreis zu g abwechselnd +1 und -1 ist. Darum ist der Flächeninhalt zu f halb so groß
wie die Umfangslänge zu f und der Flächeninhalt zu g halb so groß wie die alternierende Umfangslänge.
Man erkennt dies, wenn man die Kreiszentren mit den Eckpunkten der Vierecke verbindet und die
signierten Flächeninhalte der so gebildeten Dreiecke betrachtet.
Das Viereck mit dem blauen Startpfeil ist nicht die Summe der beiden oberen Vierecke, sondern das
Viereck zum Vektor ![]() mit einem Faktor t der in der untersten Zeile bei der Angabe der
mit einem Faktor t der in der untersten Zeile bei der Angabe der
Umgangslänge ![]() als Faktor vor
als Faktor vor ![]() auftritt. Hier wird also vor der Addition das Viereck zu f bzw. g
auftritt. Hier wird also vor der Addition das Viereck zu f bzw. g
mit dem Faktor 1 - t bzw. t gestreckt. Für die Umfangslänge gilt darum ![]() und
und
wegen der Orthogonalität der beiden oberen Vierecke ![]() . Die drei Pfeile unten
. Die drei Pfeile unten
links sind die Ortvektoren der Punkte der Ebene, deren Koordinaten die 2. und 3. Komponente der
Vierer-Vektoren ![]() ,
, ![]() und
und ![]() sind. (Aus diesen Komponenten lassen sich die 1. und 4. Komponente
sind. (Aus diesen Komponenten lassen sich die 1. und 4. Komponente
berechnen.) Da in der Gleichung ![]() die Summe der beiden Vorzahlen gleich 1 ist, bewegt
die Summe der beiden Vorzahlen gleich 1 ist, bewegt
sich in der Animation die Spitze des blauen Ortsvektors auf der Geraden durch die Spitzen des roten und
des grünen Ortsvektors.
Wenn der blaue Ortsvektor alle Punkte der schwarzen Geraden durch die Spitzen des roten und des
grünen Ortsvektors durchläuft, kommt dabei zu jedem Viereck mit den vorgegebenen Richtungswinkeln
ein ähnliches Viereck mit gleichen Richtungswinkeln vor, allerdings mit einer Ausnahme: Ein Viereck zu
einem Ortsvektor parallel zur schwarzen Gerade fehlt. Ein derartiger Vektor ist z. B. die Differenz ![]() .
.
Dieser Ausnahmefall wird in der Gleitschau nach der Animation als letztes Bild gezeigt.





Die Richtungswinkel in dieser Animation sind ![]() . Hier ist
. Hier ist
die Differenz zwischen dem ersten und zweiten Richtungswinkel größer als 180°. Wie in der vorherigen
Animation sind die beiden oberen Vierecke Tangenten-Vierecke des Einheitskreises und die signierten
Abstände des Mittelpunkts von den Seiten links alle +1 und rechts altenierend +1 und -1. Diese beiden
Vierecke sind auch hier orthogonal. Der Kreis zu f ist aber kein Inkreis. Dennoch ist die Umfangslänge
bzw. die alternierenden Umfangslänge auch hier doppelt so groß wie der Flächeninhalt.
Zur Begründung der Flächenberechnung mit Hilfe der Matrix M:
Gegeben sei ein Quadrupel ![]() mit einer monoton wachsenden Folge von Richtungswinkeln
mit einer monoton wachsenden Folge von Richtungswinkeln
im Intervall [0° ; 360°[ oder ein Quadrupel, das daraus durch zyklische Rotation entsteht. Ein Viereck mit
diesen Richtungswinkeln habe die signierten Seitenlängen ![]() , wobei
, wobei ![]() die Länge der Seite
die Länge der Seite
zum Richtungswinkel ![]() angibt.
angibt. ![]() sei der Eckpunkt zwischen den Seiten mit den Nummern j und j - 1.
sei der Eckpunkt zwischen den Seiten mit den Nummern j und j - 1.
Dabei wird die Nummer 0 mit der Nummer 4 identifiziert. Der Koordinatenursprung soll der Punkt ![]() sein.
sein.
In einer Schreibweise mit komplexen Zahlen ist dann ![]() und der signierte
und der signierte
Abstand ![]() des Punktes
des Punktes ![]() von der Seitengeraden mit der Nummer k gleich
von der Seitengeraden mit der Nummer k gleich
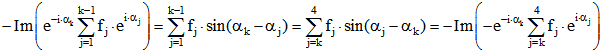 .
.
Daraus folgt ![]() . Der zum Viereck gehörige signierte Flächeninhalt
. Der zum Viereck gehörige signierte Flächeninhalt ![]()
ist die Summe der signierten Flächeninhalte der Dreiecke ![]() . Folglich ist
. Folglich ist ![]() . Dabei ist M die oben angegebenen
. Dabei ist M die oben angegebenen
Matrix ![]() mit
mit ![]() . Für den gemischten Flächeninhalt ergibt sich
. Für den gemischten Flächeninhalt ergibt sich ![]() , da M symmetrisch ist. Der Vektor der Abstände
, da M symmetrisch ist. Der Vektor der Abstände![]() ist
ist ![]() . Der entsprechenden Vektor der Abstände von den Eckpunkten
. Der entsprechenden Vektor der Abstände von den Eckpunkten![]() mit k > 1 erhält man z. B. für
mit k > 1 erhält man z. B. für ![]() , wenn man
, wenn man ![]() in der Matrix M durch
in der Matrix M durch ![]()
ersetzt und ![]() durch
durch ![]() .
.
In dem Seitenlängen-Vektor ![]() sind die Komponenten nicht voneinander unabhängig wählbar, da die
sind die Komponenten nicht voneinander unabhängig wählbar, da die
Seiten einen geschlossenen Streckenzug bilden. Zwar kann man z. B. die zweite und dritte Komponente
frei wählen. Da dann aber wegen der Vorgabe von ![]() und
und ![]() die relative Lage der Punkte
die relative Lage der Punkte ![]() ,
, ![]()
und ![]() festliegt, ist wegen der Vorgabe von
festliegt, ist wegen der Vorgabe von ![]() und
und ![]() auch die relative Lage von
auch die relative Lage von ![]() bestimmt und
bestimmt und
damit auch die Werte für ![]() und
und ![]() . Rechnerisch ergibt sich
. Rechnerisch ergibt sich ![]() mit
mit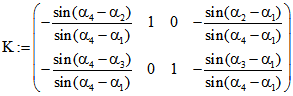 .
.
Es sei K' die transponierte Matrix, die aus K durch Vertauschung von Zeilen und Spalten entsteht.
Mit der reduzierten 2*2-Matrix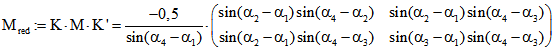
gilt dann 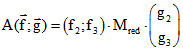 und wegen
und wegen ![]() auch
auch ![]() .
.
Sei ![]() und
und ![]() die Umfangslänge bzw. die alternierende
die Umfangslänge bzw. die alternierende
Umfangslänge des Vierecks. Dann ist ![]() mit der Matrix
mit der Matrix 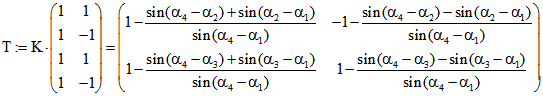 .
.
Mit ![]() gelingt die Transformation von
gelingt die Transformation von ![]() in Diagonalgestalt, nämlich in die Matrix
in Diagonalgestalt, nämlich in die Matrix
![]() mit
mit![]() und
und![]()
(In der ersten Animation ist a = 0,0480546, b = - 0,0553836
in der zweiten a = - 0,137367, b = - 0,038456.)
Es ist dann also 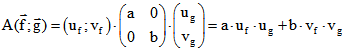 . Von besonderem Interesse
. Von besonderem Interesse
sind hierbei die Fälle ![]() und
und ![]() , die wegen der Komponente 0 nur
, die wegen der Komponente 0 nur
für Kreistangenten-Vierecke möglich sind und wegen ![]() bzw.
bzw. ![]()
nur bei einem Berührkreis mit dem Radius 1. Die zweite und die dritte Komponente von ![]() bzw.
bzw. ![]() ist dann
ist dann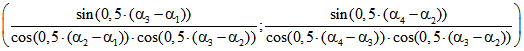 bzw.
bzw.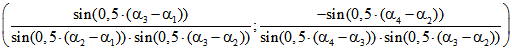 .
.
Für die Winkel der ersten Animation errechnet man daraus![]() und
und ![]()
für die der zweiten![]() und
und ![]()
Untermenü
- Drehpunktkurven
- Minkowski-Addition
- Tangenten-Pfeilecke
- orthogonale Figuren 1
- orthogonale Figuren 2
- orthogonale Figuren 3
- Addition von Vierecken ←