Es lebe die Geometrie!

Stütz-Funktion und Ko-Stütz-Funktion

Zu einer Drehpunktfunktion f mit beschränkter Variation sei die p-geschlossene Drehpunktkurve
gegeben. Die gerichtete Gerade mit dem Richtungswinkel durch
den Punkt der komplexen Ebene sei Stützgerade genannt. Sie ist eine Tangente, wenn die
Drehpunktkurve bei diesem Richtungswinkel differenzierbar ist. Der signierte Abstand der Stützgeraden
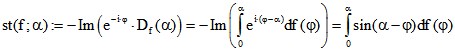vom Ursprung ist . Der
signierte Abstand des Kurvenpunktes von der zu senkrechten Geraden durch den Ursprung
ist analog 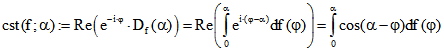. Wir nennen die
Funktionen bzw. 'Stütz-Funktion' bzw.
'Ko-Stütz-Funktion' zu f. Beide Funktionen haben beschränkte Vatiation, sind also als Differenz zweier
monotoner Funktionen darstellbar, und sind damit riemann-integrabel. Die Stütz-Funktion ist auch bei
einer unstetigen Drehpunktfunktion stetig, anders als die Ko-Stütz-Funktion. Wenn f in einem offenen
Intervall I differenzierbar ist, dann sind auch st und cst in I differenzierbar und für gilt
und .

Beipiele:
:
,

mit ganzzahligem k ungleich 1 und -1 :
,

mit ganzzahligem k ungleich 1 und -1 :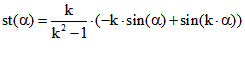
,

Diese Funktionen st und cst spielen aus folgendem Grund eine Rolle bei der Addition von Figuren. Erstens
folgen für Drehpunktfunktionen f, g und h aus h = f + g die Gleichungen und
. Außerdem kann die Bilinearform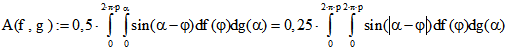

zur Berechnung des gemischten Flächeninhalt der Drehpunktkurven von f und g mit Hilfe der Stütz-Funktion
und der Ko-Stütz-Funktion berechnet werden, und zwar mit Hilfe eines Riemann-Integrals statt eines
Stieltjes-Integrals. Es gilt nämlich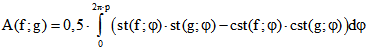
.
Der signierte Flächeninhalt der Drehpunktkurve zu f ist also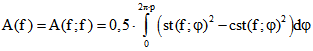
.
Für die oben angegebenen Beispiele ergibt sich nach dieser Formel im Fall p = 1:

:
oder mit ganzzahligem k ungleich 1 und -1 :
Dies sind die gleichen Werte, die man auch aus der Formel
errechnet. Da sich alle 1-periodischen Drehpunktfunktionen f mit beschränkter Variation durch
Linearkombinationen dieser Beispielfunktionen beliebig gut annähern lassen, ergeben die beiden Formeln
für alle f den gleichen Wert. Wegen gilt die Übereinstimmung
darum auch für die gemischten Flächeninhalte.

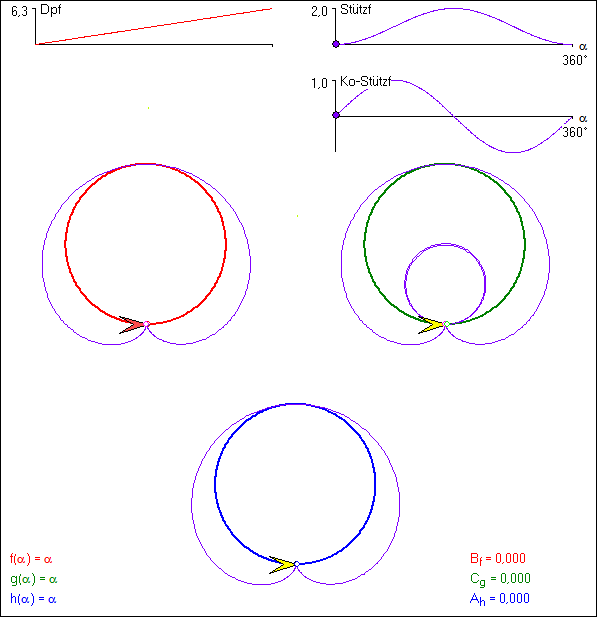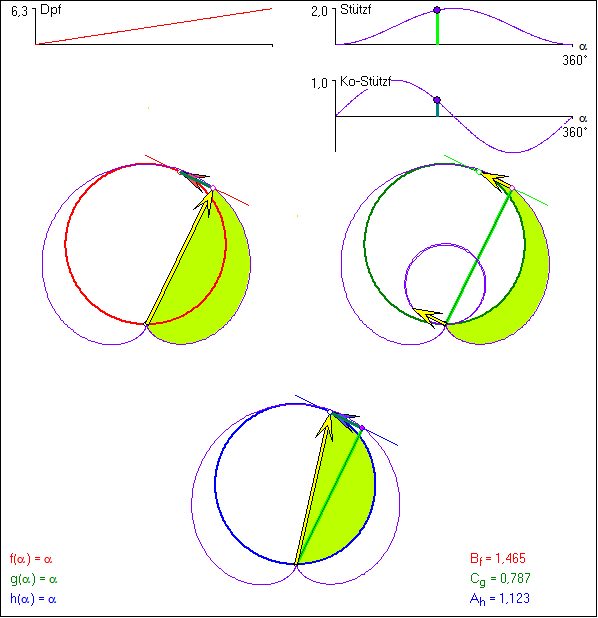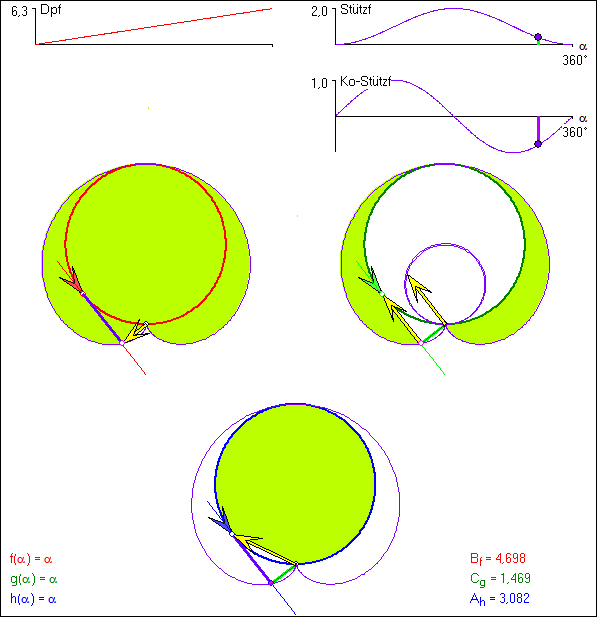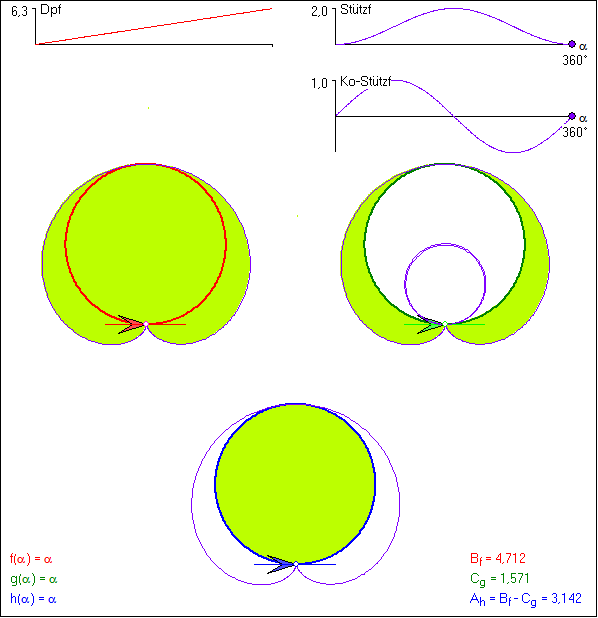
Die Animation veranschaulicht den Zusammenhang zwischen den verschiedenen Integralen zur Berechnung
von A(f) an Hand der Drehpunktfunktion , deren Drehpunktkurve der Kreis vom
Radius 1 ist. Bei der grünen Kurve wird statt f die Bezeichnung g für die gleiche Funktion benutzt und
bei der blauen die Bezeichnung h. Die Spur vom Fußpunkt L des Lots vom Ursprung U auf die Stützgerade
ist eine Kardioide. Der gelbe Pfeil beim rote Einheitskreis ist der Ortsvektor von L, dessen Länge der Betrag
von ist. Das Vorzeichen von legt fest, auf welcher Seite der Stützgeraden der
Ursprung U liegt. Beim grünen Einheitskreis ist der gelbe Pfeil der Verbindungsvektor von L mit dem
Kurvenpunkt P oder der dazu parallelgleiche Ortsektor eines Punktes auf einem Kreis vom Radius 0,5. Seine
Länge ist der Betrag von . Das Vorzeichen von bestimmt, ob P auf der Stützgeraden
vor oder hinter L liegt. Beim blauen Einheitskreis ist der gelbe Pfeil der Ortsvektor von P.

Wenn P sich auf der Drehpunktkurve bewegt, wird die von den gelben Pfeilen überstrichene Fläche farbig
markiert. Die hier benutzte Farbe ist grün, weil die Richtungswinkel der gelben Pfeile größer werden. Die
Maßzahl des Inhalts der markierten Fläche nimmt dann zu. In den folgenden Animationen kommt es vor, dass
der Richtungswinkel eines gelben Pfeils abnimmt. Dann wird eine Magenta-Färbung benutzt, weil dann der
Inhalt der markierten Fläche kleiner wird. Durch mehrmaliges Überstreichen einer Fläche wird die Markierung
dunkler oder heller, je nachdem der Betrag des Inhalts wächst oder fällt.

sei der Inhalt der Fläche, die bei der Bewegung des gelben Pfeils zwischen den Richtungswinkeln und
markiert wird. Bei der roten und bei der grünen Kurve ist näherungsweise die Hälfte des Produkts
von mit dem Quadrat der Pfeillänge, wobei der Fehler für gegen Null geht. Folglich ist der Inhalt
der gesamte markierte Fläche bei der roten Kurve und bei der grünen
. Diese Schlussweise kann man auf die blaue Kurve nur bei stetigem f übertragen,
und auch dann muss zunächst der Winkel zwischen den gelben Pfeilen zu den Tangenten-Richtungswinkeln
und bestimmt werden, denn dieser Winkel zwischen Ortsvektoren hat nicht die Größe .

Bei der blauen Kurve ergibt die Formel für den Wert
, in Übereinstimmung mit der Anschauung.

Die Animation zeigt den Zusammenhang zwischen den Integralen
, und
am Beispiel der Funktionen ,
und
.

Die Drehpunktkurven sind ein gleichseitiges Dreieck und die Quadrate Q+ und Q- mit der Seitenlänge 2.
Die zugehörigen Stütz- und Ko-Stütz-Funktionen sind

,
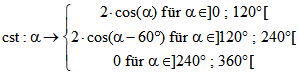
mit den Flächeninhalten , ,

,
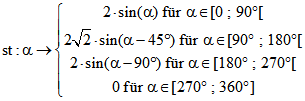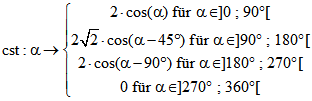
mit den Flächeninhalten , und

,
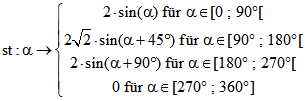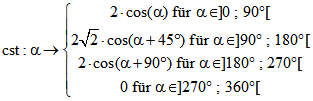
mit den Flächeninhalten , ,

Die Drehpunktfunktionen dieser Animation sind mit den Bezeichnungen der vorherigen Seite
' orthogonale Figuren 3'
,
und
.

Die Stütz-Funktionen und Ko-Stütz-Funktionen setzen sich auch hier aus Sinus-Bögen zusammen.

Die Animation zeigt die Steiner-Zykloide in zwei verschiedenen Orientierungen und ihre
Spitzen-Evolvente. Die Drehpunktfunktionen sind
,
und
.

Hier sind die Drehpunktfunktionen
und
.
Die Drehpunktkurven sind eine Astroide und eine Spitzen-Evolvente dazu.